Por pior que seja o cenário, não é possível se furtar de falar no COVID-19. O vírus que já foi comparado a uma gripezinha por diversos governantes, mas que causará a pior recessão da era republicana no Brasil. Se as previsões se confirmarem, o PIB brasileiro poderá sofrer uma queda de até 6%.
Para se ter uma ideia do que isto significa, o confisco da poupança por parte do Collor ocasionou uma queda de 4,35% em 1990. Além deste período, chegamos a cair 4,3% também em 1981, ano que Paul Volcker dobrou os juros dos EUA elevando-os de 10,94% para 20% em junho. Tal episódio provocou a moratória do Brasil e do México e marcou a década de 80 como a “década perdida”.
No site do IBGE é possível encontrar a série histórica do PIB desde de 1900, mas neste período não há quedas superiores a 3,1%. No geral, nem mesmo a quebra da bolsa de Nova Iorque em 1929, as primeiras e segundas guerras no século XX, choque dos juros, era Collor, era Dilma, enfim, todos os acontecimentos em 120 anos de história causaram o impacto que o COVID-19 irá causar. Espero, ao escrever este artigo que erremos feio nesta projeção e que a queda do PIB seja menor do que os 4,3% da década de 80.
Mas como está a evolução do COVID-19 no Brasil?
Começando pelo Estado líder nos casos, SP, pode-se verificar na figura 1 o gráfico de tendência do número de novos casos e do número de casos acumulados até agora (17/04/2020).
[caption id="attachment_39423" align="aligncenter" width="577"]
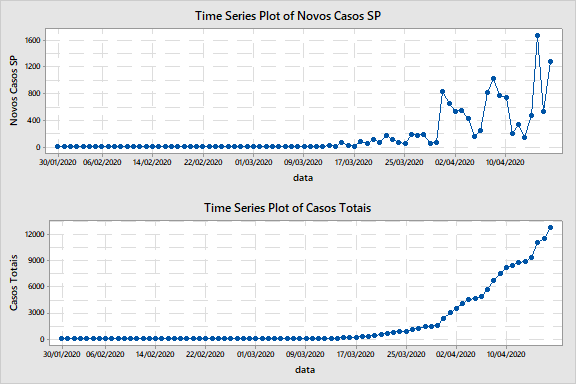Figura 1: evolução do número de casos do COVID-19 no Estado de São Paulo.[/caption]Pela figura 1 é possível notar que o crescimento dos casos está acentuado. No gráfico dos novos casos é possível identificar que a variação diária é significativa e o processo está sem controle. Na última quarta-feira, 15/04, foram reportados 1672 novos casos. Já na quinta-feira, 525. Será que o pessoal só adoece na quarta? Óbvio que não. A variação pode estar mais relacionada aos testes e confirmações. Deste modo, é melhor olhar a curva do número de casos acumulados para prever a velocidade de disseminação da doença.
Agora, como modelar a disseminação e realizar previsões de contaminação e óbitos? Como prever o custo da quarentena em relação ao aumento do número de vítimas? Como avaliar o que faz sentido? É complicado responder a estas questões e por isso, o foco do artigo será na análise técnica dos gráficos.
Um modelo de previsão para disseminação começa formulando uma hipótese sobre o poder de transmissão desta doença. Por exemplo, se uma pessoa infectada infectar mais uma pessoa apenas, a evolução pode ser dita linear. Se a lógica é 1 contamina outro, ter-se-á uma evolução linear, pois 1 contamina 1, ficando 2. O segundo, contamina um terceiro que só conseguirá contaminar um quarto. Por meio desta lógica, a previsão poderia ser feita por um modelo simples da figura 2.
[caption id="attachment_39425" align="aligncenter" width="577"]
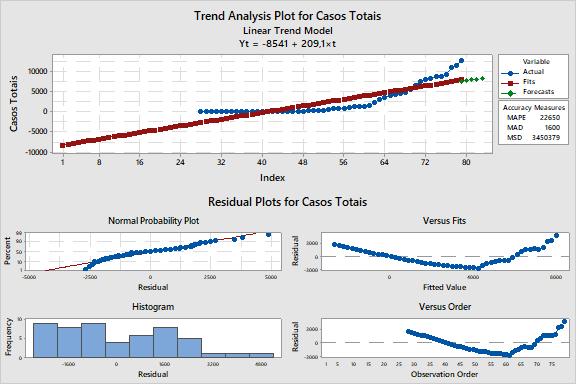Figura 2: aproximação por modelo de evolução linear da transmissão do COVID-19.[/caption]Pela figura 2 é possível identificar que esta hipótese é péssima, pois a previsão ora é menor e ora maior. Além disto, no gráfico de resíduos na parte de baixo há demonstração de viés claro. Resumindo, uma pessoa está transmitindo para mais de uma pessoa em São Paulo.
Então, como modelar a transmissão?
[caption id="attachment_39428" align="aligncenter" width="577"]
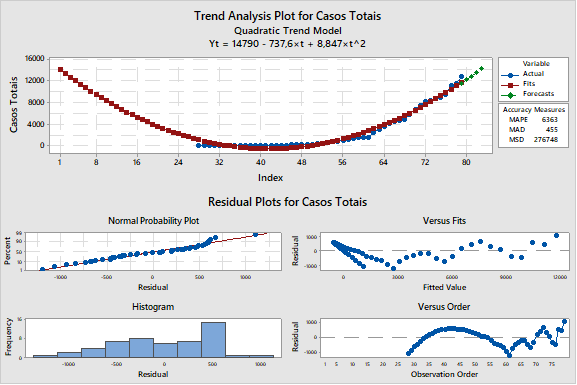Figura 3:aproximação da evolução dos casos por um modelo quadrático.[/caption]Pela figura 3, pode-se ver que o modelo gerado pela aproximação quadrática é melhor. Os resíduos estão mais controlados, mas ainda há viés. Percebe-se que a curva está evoluindo mais rápido do que o modelo do gráfico. Ou seja, não se pode utilizar este modelo para fazer previsões sobre o que acontecerá.
[caption id="attachment_39429" align="aligncenter" width="577"]
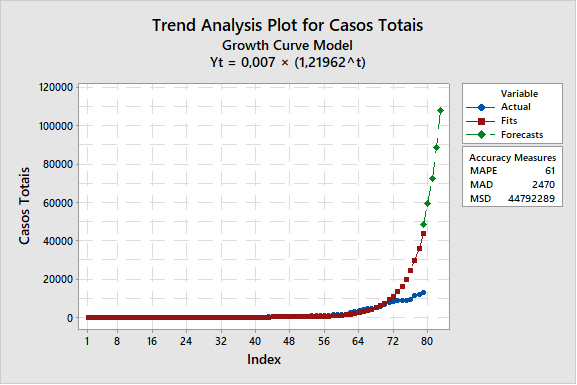Figura 4: aproximação por modelo de evolução exponencial da transmissão do COVID-19.[/caption]E se testarmos o modelo exponencial? A figura 4 responde que é pior ainda, ou seja, não é plausível tentarmos modelar uma epidemia de COVID-19 com aproximações prontas dos softwares disponíveis no mercado. É legal você utilizar a aproximação do Excel para encontrar uma linha de tendência e encaminhar para seus amigos, mas confiar nela para fazer previsões ou guiar políticas públicas, é exagero.
Para isto, deve-se elaborar modelos com um maior número de premissas e testar alguns tipos de simulações estocásticas. Há vários artigos interessantes na área e aos que desejarem se aprofundar, sugiro a leitura. Com os gráficos feitos até agora, a única coisa possível de se afirmar é que o comportamento da variável resposta (número de infectados) até agora assemelha-se mais a uma evolução quadrática, do que ao linear e ao exponencial.
Porém, um modelo bom é aquele que mapeia as variáveis de entrada também, permitindo avaliar o impacto da alteração de cada uma na variável resposta em questão. No dia 02/04/2020 a Nature publicou um relatório especial sobre as simulações da disseminação do COVID-19 em que explica resumidamente sobre o funcionamento dos modelos matemáticos de transmissão, o qual será utilizado como fonte.
Como funcionam os modelos de transmissão de doenças?
Segundo a Nature, os modelos que simulam como as doenças se espalham, se baseiam em tentar entender como as pessoas se movem entre os três estados principais:
- Indivíduos suscetíveis ao vírus (S);
- Indivíduos que foram infectados (I);
- Indivíduos que se recuperaram (R) ou morreram.
Presume-se que o grupo R seja imune ao vírus e, portanto, não pode mais transmitir a infecção. Pessoas com imunidade natural também pertenceriam a esse grupo.
Os modelos mais simples de SIR fazem suposições básicas, como que todos têm a mesma chance de pegar o vírus de uma pessoa infectada porque a população é perfeita e uniformemente misturada e que as pessoas com a doença são igualmente infecciosas até morrerem ou se recuperarem. Modelos mais avançados, que fazem as previsões quantitativas necessárias aos formuladores de políticas públicas durante uma pandemia emergente e, subdividem as pessoas em grupos menores - por idade, sexo, estado de saúde, emprego, número de contatos etc. - para definir quem encontra quem, quando e em que em quais lugares (S, I ou R).
Usando informações detalhadas sobre tamanho e densidade populacional, pirâmide etária, ligações de transporte, tamanho das redes sociais e assistência médica, os analistas constroem uma cópia virtual de uma cidade, região ou país inteiro usando equações diferenciais para controlar os movimentos e interações de grupos populacionais no espaço e no tempo. Então eles contaminam alguém do modelo com uma infecção e observam como as coisas se desenrolam.
Mas isso, por sua vez, requer informações que só podem ser estimadas com certa acuracidade no início de uma epidemia. Precisa se estimar a proporção de pessoas infectadas que morrem e o número básico de reprodução (Rt=0) - o número de pessoas, em média, para quem uma pessoa infectada passará o vírus.
E as estimativas?
O famoso modelo do Imperial College, por exemplo, estimou em seu relatório de 16 de março que:
- 0,9% das pessoas infectadas com COVID-19 morreriam (um valor ajustado à demografia específica do Reino Unido);
- o R0 estava entre 2 e 2,6;
- o SARS-CoV-2 leva 5,1 dias para incubar em uma pessoa infectada;
- pessoas que não apresentam sintomas ainda podem espalhar o vírus 4,6 dias após a infecção;
- outros podem espalhar o vírus 12 horas antes de desenvolverem sinais de doença;
- o último grupo é 50% mais infeccioso que o primeiro.
Esses números dependiam de outros tipos de modelagem. Para consegui-los os pesquisadores do Imperial recorreram a estimativas aproximadas de epidemiologistas que tentaram reunir as propriedades básicas do vírus a partir de informações incompletas em diferentes países durante os estágios iniciais da pandemia.
E os outros parâmetros?
Enquanto isso, alguns parâmetros foram totalmente assumidos. A equipe Imperial teve que supor, por exemplo, que não há imunidade natural ao COVID-19 - então toda a população começa no grupo suscetível - e que as pessoas que se recuperam do COVID-19 são imunes à reinfecção no curto prazo.
Uma execução de simulação usando esses parâmetros sempre daria a mesma previsão. Mas simulações conhecidas como modelos estocásticos injetam um pouco de aleatoriedade - como rolar um dado virtual para ver se alguém do grupo (I) infecta ou não uma pessoa (S) quando ela se encontra, por exemplo. Isso fornece uma variedade de possibilidades prováveis quando o modelo é executado várias vezes.
Os analistas também simulam as atividades das pessoas de maneiras diferentes. Nos modelos "baseados em equações", os indivíduos são classificados em grupos populacionais. Mas, à medida que os grupos são divididos em subconjuntos sociais menores e mais representativos para refletir melhor a realidade, os modelos se tornam cada vez mais complicados. Uma abordagem alternativa é usar um método 'baseado em agente', no qual cada indivíduo se move e age de acordo com suas próprias regras específicas - como os personagens do The Sims.
Modelos baseados em agentes constroem os mesmos tipos de mundo virtual que os baseados em equações, mas cada pessoa pode se comportar de maneira diferente em um determinado dia ou em uma situação idêntica.
Qual foi o modelo do Imperial College que ganhou o mundo?
A equipe do Imperial usou modelos baseados em agentes e em equações nesta pandemia. As simulações de 16 de março que a equipe realizou para informar a resposta do COVID-19 ao governo do Reino Unido usaram um modelo baseado em agentes construído em 2005 para ver o que aconteceria na Tailândia se a gripe aviária H5N1 sofresse uma mutação que pudesse se espalhar facilmente entre as pessoas.
Em 26 de março, Ferguson (líder do projeto) e sua equipe divulgaram projeções globais do impacto do COVID-19, que utiliza a abordagem mais simples baseada em equações. Ele divide as pessoas em quatro grupos: S, E, I e R, onde 'E' se refere àqueles que foram expostos, mas que ainda não são infecciosos. Por exemplo, as projeções globais sugerem que, se os Estados Unidos não tivessem tomado nenhuma ação contra o vírus, teriam ocorrido 2,18 milhões de mortes. Em comparação, a simulação anterior baseada em agentes, realizada com as mesmas premissas sobre taxa de mortalidade e número de reprodução, estimou 2,2 milhões de mortes nos EUA. Os diferentes tipos de modelo têm suas próprias forças e fraquezas.
Então, até que ponto essas simulações são confiáveis?
Segundo a Nature, durante uma pandemia, é difícil obter dados - como taxas de infecção - contra os quais julgar as projeções de um modelo. No Brasil, é nítido que o número de testes não é suficiente para cobrir toda a população infectada. Além disto, os testes realizados estão demorando até 15 dias para ficarem prontos, o que impossibilita a análise em tempo real e até a comparação da realidade com o modelo.
Os relatórios da mídia sugeriram que uma atualização do modelo do Imperial no início de março foi um fator crítico para levar o governo do Reino Unido a mudar sua política de pandemia. Os pesquisadores inicialmente estimaram que 15% dos casos hospitalares precisariam ser tratados em uma unidade de terapia intensiva (UTI), mas depois atualizaram para 30%, um valor usado na primeira divulgação pública de seus trabalhos em 16 de março. Esse modelo mostrou que o serviço de saúde do Reino Unido, com pouco mais de 4.000 leitos de UTI, ficaria sobrecarregado.
As autoridades do governo já haviam discutido uma teoria de permitir que a doença se espalhasse enquanto protegiam os mais velhos da sociedade (chamado isolamento vertical). Porque um grande número de pessoas infectadas se recuperaria e proporcionaria imunidade aos demais. Mas eles mudaram de curso ao ver as novas simulações, ordenando medidas de distanciamento social.
Os críticos então perguntaram por que o distanciamento social não havia sido discutido anteriormente, por que testes generalizados não haviam acontecido e por que os analistas haviam escolhido o número de 15%, dado que um artigo de janeiro mostrou que mais de 30% de um pequeno grupo de pessoas com O COVID-19 na China precisava de tratamento em UTI.
Ferguson diz que o significado da atualização do modelo pode ter sido exagerado. Mesmo antes disso, ele diz, os modelos já indicavam que o COVID-19, se não fosse mitigado, poderia matar na ordem de meio milhão de cidadãos do Reino Unido no próximo ano e que as UTIs iriam operar além da capacidade.
As equipes consultivas discutiram suprimir a pandemia pelo distanciamento social. Mas as autoridades estavam preocupadas com o fato de que isso só levaria a um segundo surto maior no final do ano. Testes generalizados do tipo visto na Coréia do Sul não foram considerados; mas, em parte, isso ocorreu porque a agência de saúde britânica havia dito aos assessores do governo que não seria capaz de ampliar os testes com rapidez suficiente.
E então?
Quanto aos dados chineses sobre as UTIs, os médicos os examinaram, mas observaram que apenas metade dos casos parecia precisar de ventiladores mecânicos invasivos; os outros receberam oxigênio pressurizado, por isso pode não precisariam de leitos de UTI. Com base nisso e em sua experiência com pneumonia viral, os médicos recomendaram aos analistas que considerassem 15% como uma suposição melhor.
À medida que os pesquisadores descobrem mais sobre o vírus, eles estão atualizando muitas outras variáveis-chave. No relatório de 26 março sobre o impacto global da COVID-19, a equipe do Imperial aumentou sua estimativa de 16 de março de R0 para algo entre 2,4 e 3,3; em um relatório de 30 de março sobre a propagação do vírus em 11 países europeus, os pesquisadores colocaram R0 na faixa de 3 a 4,7.
Mas algumas informações cruciais permanecem ocultas dos analistas. Um teste confiável para ver quem foi infectado sem mostrar sintomas - e, portanto, poderia ser movido para o grupo recuperado - seria um divisor de águas que poderia alterar significativamente o caminho previsto da pandemia.
Também há outra incógnita importante: como as pessoas reagirão a alterações forçadas no comportamento e se essas mudanças reduzirão os contatos infecciosos tanto quanto os cientistas esperam. Pesquisas na China, por exemplo, mostram que os cidadãos de Wuhan e Xangai relataram ter entre sete e nove vezes menos contatos diários típicos com outras pessoas durante as medidas de distanciamento social impostas pelas autoridades. Os modelos do Imperial e do LSHTM 7 parecem ter assumido mudanças nos contatos diários com o que foi observado na China, embora os relatórios de modelagem não afirmem isso claramente.
Se todos os países adotarem estratégias de distanciamento social estrito, teste e isolamento de casos infectados antes que suas mortes atinjam 0,2 por 100.000 pessoas por semana, diz a equipe do Imperial, então o total global de mortes por COVID-19 poderá ser reduzido para menos de 1,9 milhão até o final do ano.
O Estado de São Paulo já alcançou este número?
O Estado de São Paulo alcançou 368 mortes no geral na semana 16. Como o Estado tem 44 milhões de habitantes, se está longe de 0,2 por 100.000 habitantes. Para alcançar este valor seria necessário que 880 óbitos no Estado no mês. Como São Paulo adotou as medidas de isolamento precocemente quando o número alcançou 176, o caso não está perdido.
E, para concluir, reforço o apelo aos que gostam de aplicar análises ou simulações: procurem estudar os modelos SIR ou SIER seu caminho será encurtado. Por meio deles, conseguirá traçar modelos muito melhores do que apenas as simulações de Excel. Se você for da turma de Green Belts, tenho certeza de que poderá prever minimamente pelo Minitab.
Fontes
https://www.nature.com/articles/d41586-020-01003-6
https://blogdoibre.fgv.br/posts/evolucao-do-pib-capita-e-situacao-politica
https://www.medrxiv.org/content/10.1101/2020.04.04.20050328v1.article-info
