O desvio padrão é um conceito chave que desempenha um papel crucial tanto no mundo da estatística quanto no das finanças. Essa métrica não é apenas essencial para calcular a variabilidade em uma amostra de pesquisa, mas também serve como uma ferramenta de avaliação de risco amplamente utilizada por analistas financeiros, gestores de carteiras e consultores.
Entender o desvio padrão ajuda a interpretar dados de forma mais eficaz, e a tomar decisões de investimento mais informadas.
Neste blog, exploraremos em detalhe o que é, como ele é utilizado em diferentes contextos e forneceremos um guia passo a passo sobre como calculá-lo eficientemente.
Se você deseja aprimorar sua habilidade analítica ou simplesmente entender melhor os riscos associados aos seus investimentos, continue lendo para descobrir como essa poderosa ferramenta estatística pode ser aplicada.
O que é desvio padrão?
Desvio padrão é uma medida de dispersão usada em estatística para mostrar o quanto os valores de um conjunto de dados variam em relação à média. Ele quantifica o grau de afastamento dos dados em relação ao valor central.
Quando o desvio padrão é baixo, os dados estão próximos da média. Se for alto, os valores estão mais espalhados. Essa medida permite avaliar a consistência dos dados e a variabilidade dentro do conjunto.
É comum usar o desvio padrão para identificar padrões de comportamento, variações incomuns (outliers) e estimar o nível de precisão de uma análise estatística.
Fórmula do desvio padrão
O desvio padrão é um componente fundamental no cálculo do tamanho da amostra da pesquisa. A fórmula para calculá-lo é a seguinte:
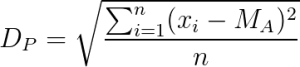
- Dp = desvio padrão
- ∑ = soma de
- Xi = cada valor
- Ma = média aritmética
- n = quantidade de dados
Diferença entre variância e desvio padrão
A variância, bem como o desvio também é uma medida de dispersão que indica a regularidade de um conjunto de dados em torno da média. Ela é semelhante ao próprio desvio padrão uma vez que um deriva-se do outro. A variância é calculada como o quadrado do desvio padrão, que resulta basicamente na exclusão da raiz quadrada da fórmula do desvio padrão.
Variância: mede a dispersão absoluta dos valores.
Desvio padrão: mede a dispersão na mesma unidade dos dados originais.
Como calcular o desvio padrão de uma amostra?
Calcular o desvio padrão de uma amostra é um processo detalhado que envolve várias etapas matemáticas para avaliar a dispersão dos dados em relação à sua média. Aqui está um guia mais completo para calcular o desvio padrão de uma amostra de pesquisa:
1. Calcule a média dos pontos de dados
Primeiramente, determine a média aritmética do conjunto de dados. Isso é feito somando todos os valores dos pontos de dados e, em seguida, dividindo essa soma pelo número total de pontos. A média serve como o ponto central dos dados, contra o qual as variações serão medidas.
2. Determine a variação de cada ponto de dados
Subtraia a média calculada no passo 1 de cada ponto de dados individual. Esse cálculo mostra a diferença entre cada ponto de dados e a média, fornecendo uma medida de quão longe cada ponto está do centro dos dados.
3. Eleve ao quadrado cada variação obtida
Para eliminar quaisquer problemas causados por diferenças negativas (já que a direção da diferença não é importante, apenas a magnitude), eleve ao quadrado cada resultado da variação obtido no passo 2. Isso resulta em valores de variância quadrada que são sempre positivos.
4. Some todas as variâncias quadradas
Adicione todos os valores de variância quadrada obtidos no passo 3. Esta soma representa a variância total dos pontos de dados em relação à média, ajustada para o tamanho da amostra.
5. Divida pelo número de pontos de dados menos um
O próximo passo é dividir a soma das variâncias quadradas pelo número de pontos de dados menos um (n-1). Esta etapa é crucial porque usa um denominador de (n-1) em vez de n, um método conhecido como correção de Bessel, que compensa o fato de que apenas uma amostra da população total está sendo usada e fornece uma estimativa mais precisa da variância da população total.
6. Calcule a raiz quadrada do resultado
Finalmente, tire a raiz quadrada do quociente obtido na etapa 5. O resultado é o desvio padrão da amostra, que quantifica a quantidade de dispersão ou variabilidade dos pontos de dados em relação à média.
Entender e calcular corretamente o desvio padrão permite aos pesquisadores e analistas fazer inferências mais precisas sobre seus dados e tomar decisões mais informadas.
Como interpretar o desvio padrão?
Interpretar o valor do desvio padrão envolve entender como os dados estão dispersos em relação à média do conjunto de dados. A seguir estão algumas orientações para ajudar na interpretação do desvio padrão:
- Desvio padrão igual a zero: isso significa que todos os valores do conjunto de dados são iguais à média e não há variação. Os dados são perfeitamente uniformes;
- Desvio padrão baixo: um desvio padrão baixo indica que a maioria dos valores do conjunto de dados está próxima da média. Os dados são menos dispersos e estão concentrados em torno da média;
- Desvio padrão alto: um desvio padrão alto sugere que os valores estão mais distantes da média e há uma maior dispersão dos dados.
Para uma interpretação mais concreta, é possível utilizar a regra empírica de 68-95-99,7, que é válida para conjuntos de dados com distribuição normal (ou aproximadamente normal):
- 68% dos dados estão dentro de 1 desvio padrão da média;
- 95% dentro de 2 desvios padrão da média;
- 99,7% dentro de 3 desvios padrão da média.
Lembre-se de que a aplicabilidade dessa regra depende da distribuição dos dados. Se os dados não seguirem uma distribuição normal, a regra pode não se aplicar diretamente. Em geral, o desvio padrão é uma ferramenta útil para compreender a dispersão dos dados, identificar outliers e avaliar a precisão de estimativas estatísticas.
Quer desenvolver habilidades analíticas e tomar decisões mais estratégicas com dados? No curso gratuito de Fundamentos da Ciência de Dados da FM2S, você aprende conceitos essenciais de estatística e análise de dados de forma prática e acessível. Inscreva-se e comece agora a transformar informação em vantagem competitiva!

Exemplo de desvio padrão em pesquisa de melhoramento genético de plantas
Um pesquisador está avaliando o desempenho de cinco variedades de milho geneticamente modificadas. O objetivo é analisar a variação da altura das plantas (em centímetros), medida após 90 dias do plantio.
As alturas médias de cinco amostras de plantas, uma de cada variedade, foram:
145, 150, 147, 152, 146
Vamos calcular o desvio padrão amostral para entender o quanto essas alturas variam entre si.
1. Calcular a média das alturas:
Somamos todos os valores observados:
Soma = 145 + 150 + 147 + 152 + 146 = 740
Depois, dividimos pelo número total de amostras:
Média = 740 ÷ 5 = 148 cm
2. Calcular os desvios em relação à média e elevar ao quadrado:
Agora, verificamos o quanto cada valor se distancia da média (148 cm) e elevamos esses desvios ao quadrado para eliminar os sinais negativos:
(145 - 148)² = 9
(150 - 148)² = 4
(147 - 148)² = 1
(152 - 148)² = 16
(146 - 148)² = 4
Esses valores representam o grau de dispersão de cada medida em relação à média.
3. Calcular a variância amostral:
Somamos os quadrados obtidos:
Soma dos quadrados = 9 + 4 + 1 + 16 + 4 = 34
Dividimos esse total por (n − 1), ou seja, 5 − 1 = 4. Isso é chamado de correção de Bessel, usada para amostras:
Divisão por (n - 1): 34 ÷ 4 = 8,5
4. Calcular o desvio padrão:
Por fim, aplicamos a raiz quadrada da variância para voltar à unidade original (centímetros):
√8,5 ≈ 2,91 cm
Interpretação: esse valor mostra que, em média, a altura das plantas varia cerca de 2,91 cm em relação à média de 148 cm, o que indica que as variações entre as variedades são relativamente baixas. Isso é útil para comparar a uniformidade entre os genótipos avaliados e apoiar decisões sobre quais materiais devem seguir para novas fases de teste.





