Intervalos de confiança para avaliar a variação do teor de gordura de hambúrgueres em um restaurante de Fast Food
Hamburrgerr, Inc. é um restaurante de fast food que serve hambúrgueres entre alguns outros itens. O restaurante afirma que o teor médio de gordura nos hambúrgueres é de 15 gramas.
A seção 1 fornece uma breve descrição da fase Define. A seção 2 ilustra a fase Measure com instruções detalhadas para o uso do Minitab®. A fase Analyse é brevemente discutida na Seção 3. A Seção 4 ilustra a fase Improve com instruções as instruções do Minitab®. Finalmente, a fase Control é brevemente discutida na Seção 5.
Define
Alguns clientes reclamaram recentemente ao gerente de operações da Hamburrgerr, Inc que a quantidade de gordura nos hambúrgueres parecia ser maior do que anunciado pelo restaurante (15 gramas). O gerente de operações deseja usar intervalos de confiança de 95% para verificar se o valor médio de 15 gramas de gordura nos hambúrgueres é de fato correto. Ele também deseja verificar sua suposição de que o desvio padrão do teor de gordura é inferior a 1 grama.
Measure
O gerente de operações seleciona aleatoriamente 20 hambúrgueres e mede o teor de gordura (em gramas) em cada um deles, obtendo os seguintes resultados: 15,5, 12,3, 15,4, 16,5, 15,9, 17,1, 16,9, 14,3, 19,1, 18,2, 18,5, 16,3, 20,0, 19,0, 15,6, 13,5, 14,0, 16,5, 19,0 e 18,6 (caso deseje seguir o passo-a-passo, insira esses dados em uma worksheet do Minitab® e nomeie a variável como “Gordura”)
Antes de construir um intervalo de confiança para os dados acima, é importante verificar se os dados estão no controle estatístico. Como cada número é para um hambúrguer, o conjunto apropriado de cartas de controle são os gráficos I-AM (intervalo individual e amplitude móvel). É apresentada na Figura 1 como selecionar gráficos I-AM no Minitab®. Isso vai abrir a caixa de diálogo apresentada na Figura 2. Selecione "Gordura" para "Variáveis" e clique em "OK". Os gráficos de I-AM mostrados na Figura 3 serão o resultado. Como é possível observar, os dados estão no controle estatístico, ou seja, o processo está estável.
Figura 1 – Seleção do gráfico de controle I-AM antes da melhoria.
Figura 2 - Variável de "Gordura" para o gráfico I-MR antes da melhoria
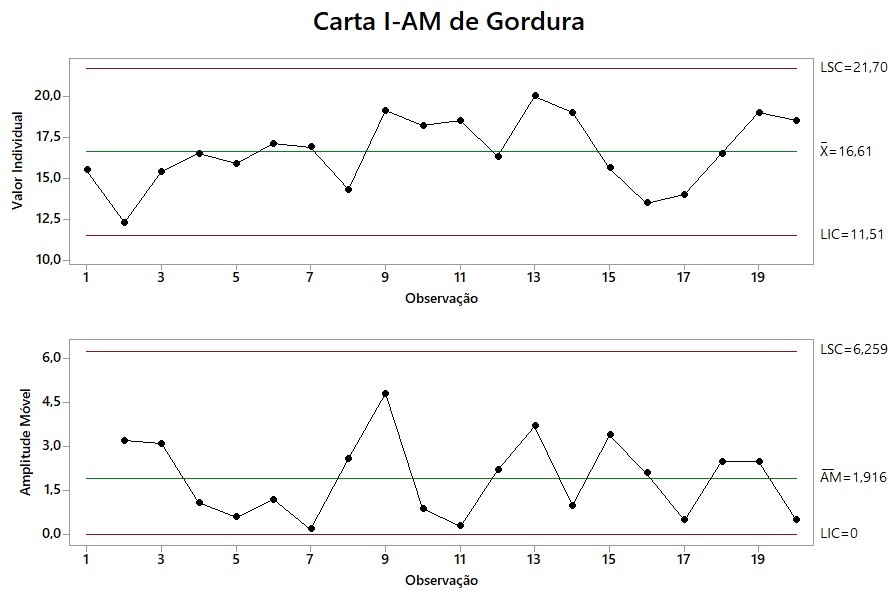
Figura 3 - Gráficos I-AM antes da melhoria
Garantido o controle estatístico dos dados, o gerente deseja então construir o intervalo de confiança de 95% para a média do teor de gordura na população de hambúrgueres. Contudo, para uma correta análise, ele resolve também verificar a normalidade do conjunto de dados.
A opção "Sumário Gráfico" no Minitab® produz tanto o resultado do teste de normalidade quanto o intervalo de confiança. É apresentada na Figura 4 como selecionar essa opção. Ao fazê-lo, abrirá no Minitab® a caixa de diálogo apresentada na Figura 5. Selecione "Gordura" para "Variáveis" e clique em "OK".

Figura 4 -Seleção do "Sumário Gráfico" antes da melhoria.
Figura 5 - Variável de "Gordura" para resumo gráfico antes da melhoria
O resultado do Sumário Gráfico é apresentado na Figura 6. Como P-valor (0,624) do teste de normalidade de Anderson-Darling é maior do que 0,05, então os dados são normalmente distribuídos. Observe que a média da população é estimada entre 15,625 gramas e 17,595 gramas. Todo o intervalo de confiança (de 15,625 a 17,595) é maior do que os 15 gramas, portanto, o gerente de operações vai precisar tomar alguma medida para resolver esse problema.
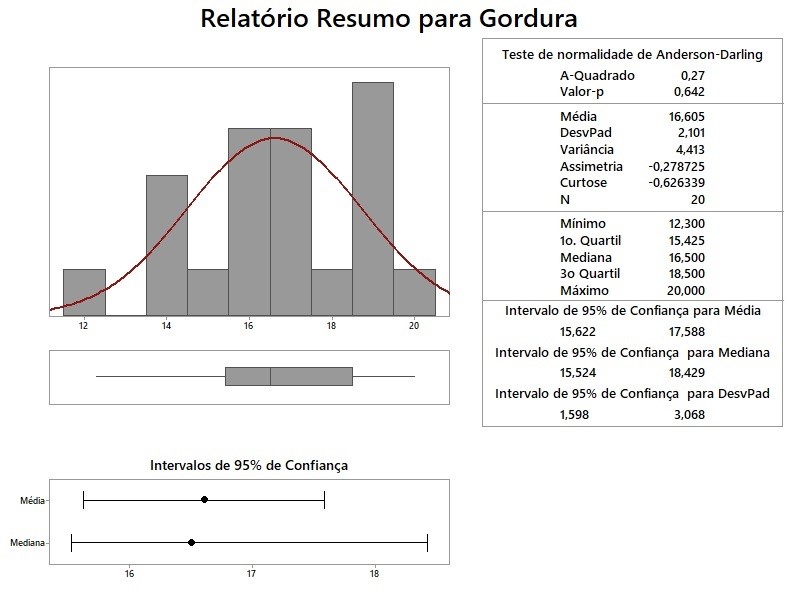
Figura 6 - Sumário gráfico antes da melhoria
O gerente então resolve verificar sua suposição de que o desvio padrão do teor de gordura é inferior a 1 grama. É apresentada na Figura 7 como selecionar "Teste para 1 Variância" no Minitab®. Ao fazê-lo, abrirá a caixa de diálogo apresentada na Figura 8. Selecione "Uma ou mais amostras, cada uma em uma coluna" para "Dados" e "Gordura" para "colunas".
Clique em "Opções" para abrir a caixa de diálogo apresentada na Figura 9. Selecione "Desvio padrão < desvio padrão hipotético” para "Hipótese alternativa" porque o gerente está interessado em verificar se o desvio padrão é inferior a 1 grama. Clique em "OK" e você volta à caixa de diálogo da Figura 8. Clique em "OK" e o resultado é apresentado no pergaminho do Minitab®, como observado na Figura 10.
Como os dados são normalmente distribuídos, devemos observar o limite superior (2,88 gramas) do desvio padrão dado pelo método do qui-quadrado. Isso significa que 95% dos hambúrgueres têm conteúdo de gordura com um desvio padrão inferior a 2,88 gramas, valor este muito maior do que a hipótese de 1 grama. O gerente de operações também considera isso uma questão muito séria.
Figura 7 -Seleção de "Teste para 1 Variância" antes da melhoria
Figura 9 - Seleção de opção "menor que" para estimar o desvio padrão antes da melhoria

Figura 10 - Intervalo de confiança de 95% de uma variância para o desvio padrão antes da melhoria
Antes de focar nas mudanças, o gerente deseja verificar a quantidade de clientes insatisfeitos. Para este fim, seleciona aleatoriamente 1000 clientes que compraram hambúrgueres e descobre que 83 deles estão insatisfeitos com a qualidade dos alimentos. Ele então começa a construir um intervalo de confiança para a proporção de todos os clientes que estão insatisfeitos. É apresentada na Figura 11 como selecionar "Teste para 1 Proporção" no Minitab®. Ao fazê-lo, abrirá a caixa de diálogo mostrada na Figura 12.
Mas que a opção “Dados Sumarizados” e digite "83" para "Número de eventos" e "1000" para "Número de testes". Clique em "Opções" e abre a caixa de diálogo mostrada naFigura 13. Selecione "Proporção < proporção hipotética" para "Hipótese alternativa" porque o gerente de operações está interessado em reduzir a proporção de todos os clientes que não estão satisfeitos. Além disso, selecione em “Método” a opção “Aproximação normal". Clique em "OK" e o leva de volta à caixa de diálogo mostrada na Figura 12. Clique em "OK" e a saída mostrada na Figura 14 é o resultado. É claro que existe uma probabilidade de 95% de que a proporção de todos os clientes que estão insatisfeitos é inferior a 0,097 (ou 9,7%). O gerente de operações deseja então diminuir essa estimativa do limite superior.
Figura 11 – Seleção de "Teste para 1 Proporção" antes da melhoria
Figura 12- Entrada de "Número de eventos" e "Número de ensaios" antes da melhoria
Figura 13- Seleção de opção "Proporção < proporção hipotética" para estimar a proporção da população antes da melhoria e “Aproximação normal” para “Método”.

Figura 14- Intervalo de confiança de 95% para uma variância para a proporção da população antes da melhoria
Analyze
O gerente de operações analisa o processo e descobre que a quantidade de gordura e sua variação são altamente afetados pela quantidade de óleo usada pelos empregados nas três diferentes grelhas usadas para fazer hambúrgueres.
Improve
O gerente de operações padroniza o processo para que o uso de óleo nas três grelhas diferentes seja controlado. Uma máquina automática é comprada e instalada para distribuir óleo em uma grelha cada vez que um hamburguer é feito. Para verificar se o processo realmente melhorou, o gerente de operações selecionou aleatoriamente 20 hambúrgueres e mediu o teor de gordura (em gramas) em cada um deles, obtendo os seguintes: 14,9, 15,0, 15,4, 15,3, 15,2, 15,1, 14,9, 14,8, 15.6, 14,5, 15,3, 15,8, 15,0, 15,0, 14,3, 15,3, 15,2, 14,7, 15,1 e 14,7.
Assim como na fase do Measure, antes de construir um intervalo de confiança para os dados acima, é importante verificar se os dados estão no controle estatístico. Como cada número é para um hamburger, a carta de controle apropriada é novamente a I-AM. Como apresentado na Figura 15, os dados estão dentro do controle estatístico.
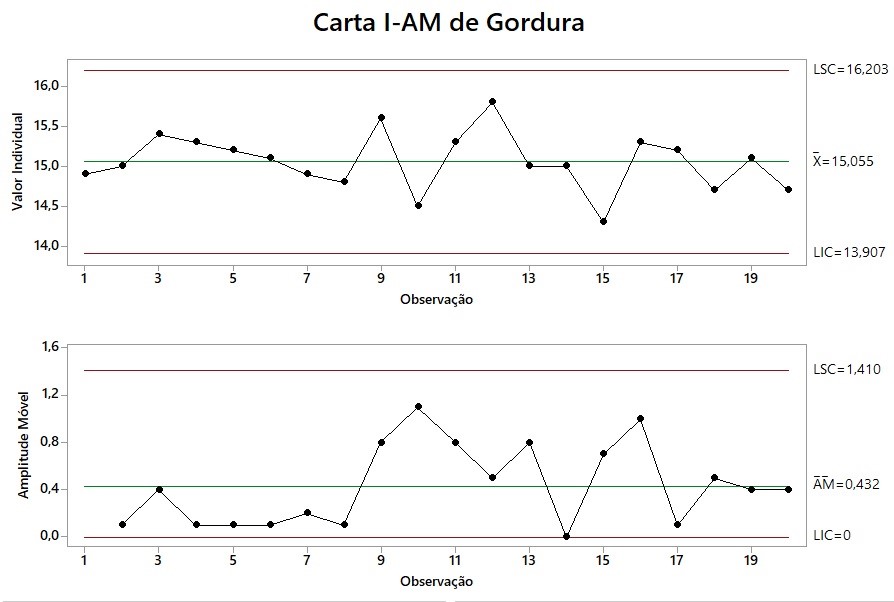
Figura 15 - Carta de controle I-AM realizada depois da melhoria
Depois de checada a estabilidade do processo, o gerente de operações deseja construir o intervalo de confiança de 95% para a média do teor de gordura na população de hambúrgueres. Como feito na fase Measure, ele também deseja verificar se os dados são normalmente distribuídos antes de analisar intervalo de confiança. É apresentado na Figura 16 o resultado do Sumário Gráfico. Como o P-Valor (0,925) do teste de normalidade Anderson-Darling é superior a 0.05, os dados são normalmente distribuídos. Observe que a média da população é estimada entre 14,887 gramas e 15,223 gramas. Na medida em que o valor de 15 gramas está dentro do intervalo (14,887; 15,223), fica claro que houve melhoria do processo em relação ao teor médio de gordura.
O gerente de operações então resolve verificar sua hipótese de que o desvio padrão do teor de gordura é inferior a 1 grama. Como possível observar a partir da saída mostrada na Figura 17, o limite superior é 0,492 gramas para o desvio padrão (dado pelo método do qui-quadrado). Isso significa que 95% dos hambúrgueres têm conteúdo de gordura com um desvio padrão inferior a 0,492 gramas. Como 0,492 grama é inferior ao pressuposto de 1 grama, então o processo melhorou em relação ao desvio padrão também.
Pode-se simular intervalos de confiança usando o Minitab®. O gerente de operações deseja realizar a simulação para 10 amostras normalmente distribuídas com um tamanho de amostra de 20 hambúrgueres. Fazendo o que é mostrado na Figura 18, o Minitab® abre a caixa de diálogo apresentada na Figura 19. Selecione "20" para "Número de linhas de dados a serem geradas". Digite "C3-C12" para "Armazenar na (s) coluna (s)". Como, após a melhoria do processo, a população significa aproximadamente 15 gramas e o desvio padrão da população é de aproximadamente 0,5 gramas, digite "15" para "média" e "0,5" para "Desvio padrão". Clique em "OK" e o resultado é mostrado na Figura 20. (Obs.: Como estão sendo gerados dados aleatórios, os gráficos apresentados podem ser ligeiramente diferentes daqueles que você obteve, porém, sem prejuízo dos resultados.)
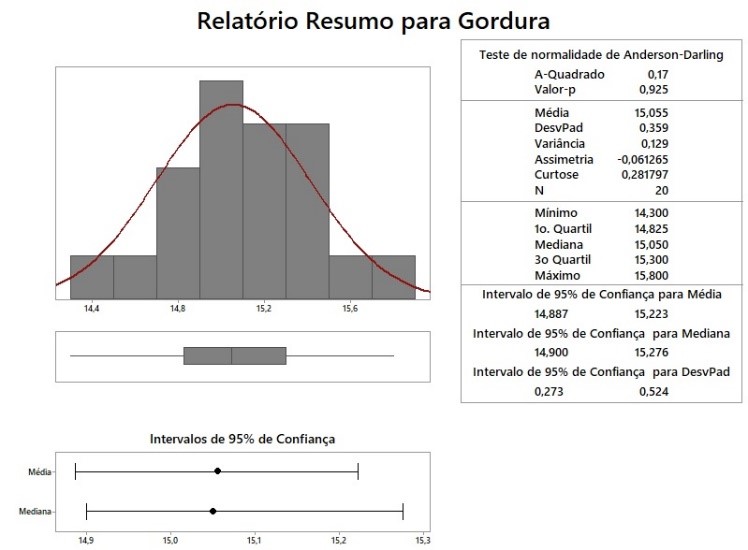
Figura 16 - Sumário Gráfico após a realização da melhoria.

Figura 17 - Intervalo de confiança para uma variância de 95% para o desvio padrão após a melhoria.
Figura 18 - Seleção para gerar dados normalmente distribuídos
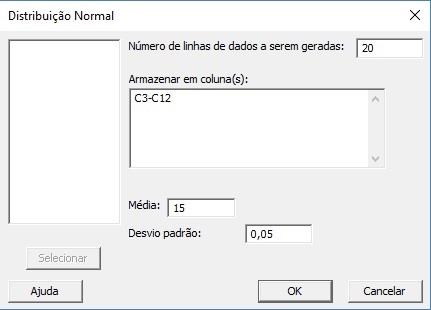
Figura 19 – Definição de Média e desvio padrão para a geração de amostras aleatórias
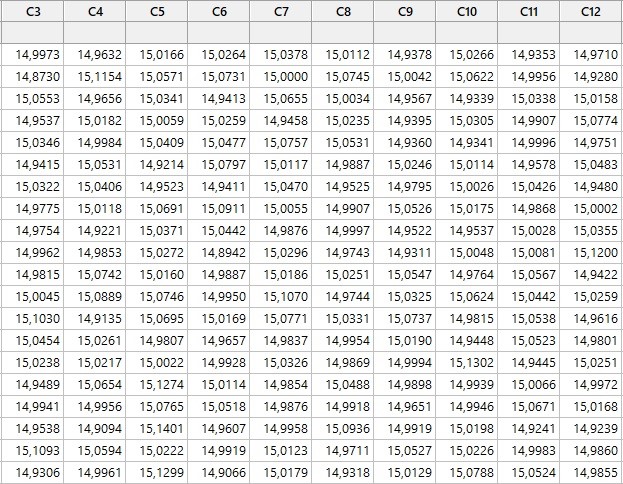
Figura 20 - Dez amostras aleatórias com tamanho igual a 20
Antes de proceder à simulação, é uma boa prática é verificar se os dados gerados estão no controle estatístico. Como o tamanho da amostra é maior que 10, os gráficos de controle apropriados são gráficos Xbarra-S (médias e desvios padrão da amostra). É apresentado na Figura 21 como selecionar os gráficos "Xbarra-S". Isso abrirá a caixa de diálogo mostrada na Figura 22. Selecione "Observações para um subgrupo estão em uma linha de colunas" no menu suspenso e selecione "C3-C12" na caixa vazia abaixo do menu. Clique em "OK" e os gráficos Xbarra-S mostrados na Figura 23 são o resultado. É possível observar que os dados estão em controle estatístico.

Figura 21 – Seleção de "Xbarra-S"
Figura 22 – Seleção de variáveis para gráficos Xbarra-S

Figura 23 -Gráfico “Xbarra-S”
Para simular os intervalos de confiança para as 10 amostras geradas, selecione "Gráfico de Intervalos", como mostrado na Figura 24. Fazendo assim, o Minitab® abre a caixa de diálogo mostrada na Figura 25. Selecione "Simples" em "Vários Ys" e clique em "OK". Isso abrirá a caixa de diálogo mostrada na Figura 26. Selecione as colunas "C3-C12" para "Variáveis de gráfico" e clique em "OK". O intervalo de intervalos (intervalos de confiança de 95%) para as 10 amostras mostradas na Figura 27 são criados.
Figura 24- Seleção de "Gráfico de Intervalos" para simulação de intervalos de confiança
Figura 25 - Seleção de Gráfico de Intervalos "Simples" em "Múltiplos Y’s"
Figura 26 - Seleção de variáveis para simulação
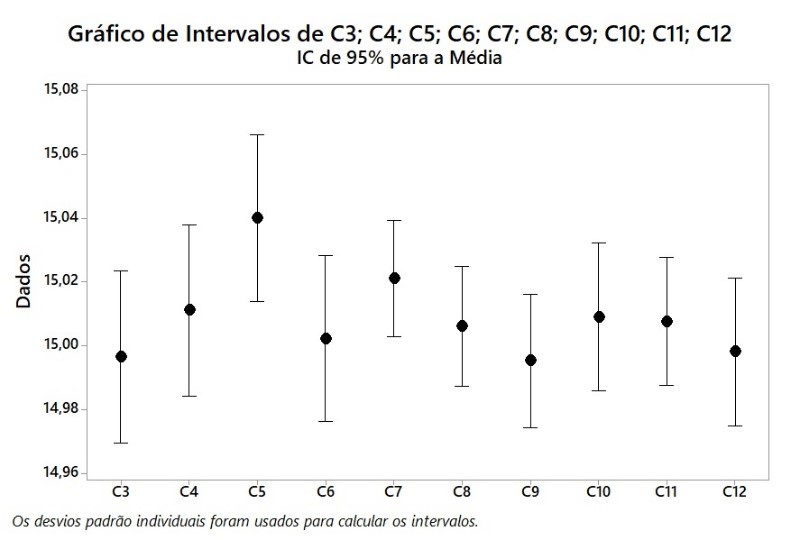
Figura 27 – Gráfico de intervalos sem linha de referência
Conforme mostrado na Figura 28, clique com o botão direito do mouse em qualquer lugar no gráfico do intervalo e selecione "Linhas de Referência". Isso abrirá a caixa de diálogo apresentada na Figura 29. Digite "15" para "Mostrar linhas de referência em valores Y" e clique em "OK". Isso adiciona a linha de referência de 15, como mostrado na Figura 30. Como a maioria dos intervalos de confiança contém a média da população de 15 gramas, esta simulação confirma que a estimativa média da população é de fato de 15 gramas. Se a simulação for realizada para um grande número de amostras, espera-se que 95% dos intervalos de confiança conterão o valor de 15 gramas.
Figura 28 -Processo para mostrar a linha de referência
Figura 29 – Entrada do valor da linha de referência
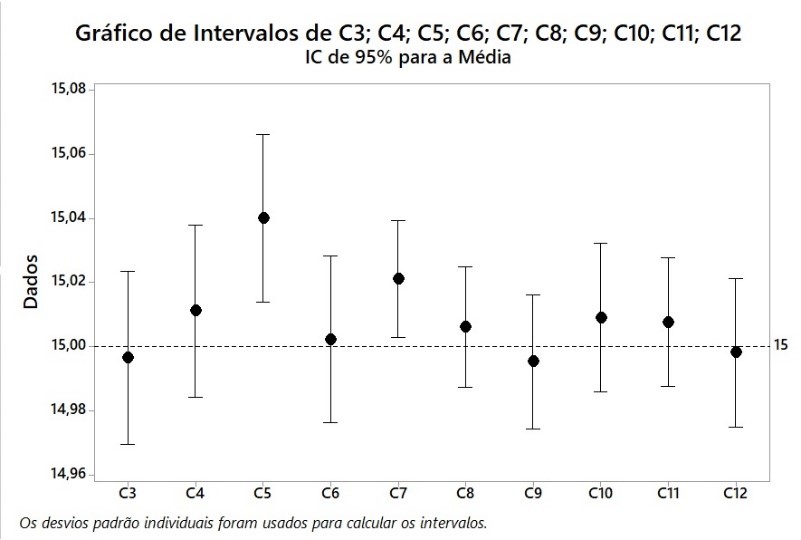
Figura 30 -Gráfico de intervalo com linha de referência
O gerente de operações agora deseja verificar quantos dos clientes estão insatisfeitos após o processo ter melhorado. Para este fim, ele seleciona aleatoriamente 1200 clientes que compraram hambúrgueres e verifica que 25 deles estão insatisfeitos com a qualidade dos alimentos. Ele então resolve construir um intervalo de confiança para a proporção de todos os clientes que estão insatisfeitos. Na caixa de diálogo mostrada na Figura 31, digite "25" para "Número de eventos" e "1200" para "Número de testes". Clique em "Opções". Em “Hipótese alternativa” selecione “proporção < proporção hipotética” e em “Método” selecione “Aproximação normal”. Isso porque o gerente de operações está interessado em diminuir a proporção de todos os clientes que não estão satisfeitos. Clique em "OK" e você de voltará à caixa de diálogo mostrada na Figura 31. Clique em "OK" e o resultado será igual ao apresentado na Figura 32. Fica evidente que a probabilidade de 95% de que a proporção de todos os clientes que estão insatisfeitos é inferior a 0,027 (ou 2,7%). O gerente de operações está convencido de que o processo melhorou.
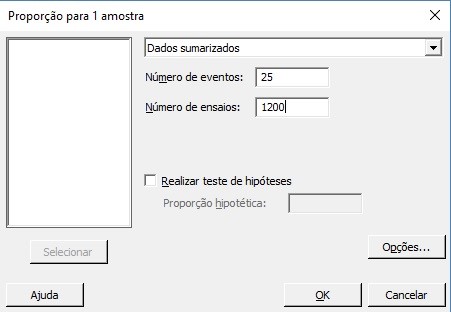
Figura 31 – Entrada do número de eventos e ensaios após a melhoria

Figura 32 – Intervalo de confiança de 95% para uma variância para a proporção da população após a melhoria
Control
O gerente de operações planeja verificar regularmente o processo de preparação de hambúrguer nas três grelhas, a fim de garantir que os clientes recebam consistentemente o que lhes é prometido.





