O desvio padrão é um conceito-chave que desempenha um papel crucial tanto no mundo da estatística quanto no das finanças. Essa métrica não é apenas essencial para calcular a variabilidade em uma amostra de pesquisa, mas também serve como uma ferramenta de avaliação de risco amplamente utilizada por analistas financeiros, gestores de carteiras e consultores.
Entender o desvio padrão ajuda a interpretar dados de forma mais eficaz, e a tomar decisões de investimento mais informadas.
Neste blog, exploraremos em detalhe o que é o desvio padrão, como ele é utilizado em diferentes contextos e forneceremos um guia passo a passo sobre como calculá-lo eficientemente.
Se você deseja aprimorar sua habilidade analítica ou simplesmente entender melhor os riscos associados aos seus investimentos, continue lendo para descobrir como essa poderosa ferramenta estatística pode ser aplicada.
O que é desvio padrão?
O desvio padrão é uma medida de dispersão ou variabilidade em estatísticas e probabilidade. Ele indica o grau de variação ou dispersão dos dados em um conjunto em relação à média (valor médio) desse conjunto. Em outras palavras, o desvio padrão ajuda a entender o quão distantes os valores individuais estão da média.
Um desvio padrão baixo sugere que a maioria dos dados está concentrada em torno da média, enquanto um desvio padrão alto indica que os dados estão mais espalhados. O desvio padrão é frequentemente utilizado para identificar padrões, anomalias ou outliers em conjuntos de dados e para entender a incerteza ou precisão das estimativas estatísticas.
Importância do desvio padrão
O desvio padrão é um fator chave para a análise estatística . Algumas razões para isso são:
- Inclui todas as observações
Um benefício do viés é que todos os pontos de dados são incluídos na análise. Outras medidas de desvio, como o alcance, medem apenas os pontos mais dispersos, sem levar em conta os pontos intermediários. Portanto, o desvio padrão é frequentemente considerado uma medida mais robusta e precisa em comparação com outras observações.
- Pode ser usado em combinação
O desvio padrão de dois conjuntos de dados pode ser combinado usando uma fórmula específica de desvio combinado. Não existem fórmulas semelhantes para outras medidas observacionais de dispersão nas estatísticas. Além disso, o desvio padrão pode ser utilizado em outros cálculos algébricos, ao contrário de outros meios de observação.
- Permite saber quando um conjunto está distribuído de forma desigual
A inclinação é especialmente útil se você quiser saber até que ponto o seu conjunto de dados está distribuído de forma desigual. Ele informa não apenas a dispersão dos seus dados, mas também sua distribuição desigual.
- Permite realizar análises matemáticas e estatísticas
O valor do desvio padrão é sempre fixo e bem definido, portanto através dele é possível realizar análises tanto matemáticas quanto estatísticas.
- Permite conhecer a volatilidade de um investimento
A volatilidade de um investimento pode ser determinada pelo número de pontos de dados que se desviam da média. Quanto mais os pontos de dados se desviarem da média, mais volátil será o investimento.
Quer desenvolver habilidades analíticas e tomar decisões mais estratégicas com dados? No curso gratuito de Fundamentos da Ciência de Dados da FM2S, você aprende conceitos essenciais de estatística e análise de dados de forma prática e acessível. Inscreva-se e comece agora a transformar informação em vantagem competitiva!

Fórmula do desvio padrão
O desvio padrão é um componente fundamental no cálculo do tamanho da amostra da pesquisa. A fórmula para calculá-lo é a seguinte:
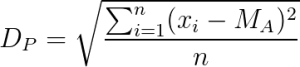
- Dp = desvio padrão
- ∑ = soma de
- Xi = cada valor
- Ma = média aritmética
Diferença entre variância e desvio padrão
A variância, bem como o desvio também é uma medida de dispersão que indica a regularidade de um conjunto de dados em torno da média. Ela é semelhante ao próprio desvio padrão uma vez que um deriva-se do outro. A variância é calculada como o quadrado do desvio padrão, que resulta basicamente na exclusão da raiz quadrada da fórmula do desvio padrão.
Variância: mede a dispersão absoluta dos valores.
Desvio padrão: mede a dispersão na mesma unidade dos dados originais.
Como calcular o desvio padrão de uma amostra?
Calcular o desvio padrão de uma amostra é um processo detalhado que envolve várias etapas matemáticas para avaliar a dispersão dos dados em relação à sua média. Aqui está um guia mais completo para calcular o desvio padrão de uma amostra de pesquisa:
- Calcule a média dos pontos de dados: primeiramente, determine a média aritmética do conjunto de dados. Isso é feito somando todos os valores dos pontos de dados e, em seguida, dividindo essa soma pelo número total de pontos. A média serve como o ponto central dos dados, contra o qual as variações serão medidas.
- Determine a variação de cada ponto de dados: subtraia a média calculada no passo 1 de cada ponto de dados individual. Esse cálculo mostra a diferença entre cada ponto de dados e a média, fornecendo uma medida de quão longe cada ponto está do centro dos dados.
- Eleve ao quadrado cada variação obtida: para eliminar quaisquer problemas causados por diferenças negativas (já que a direção da diferença não é importante, apenas a magnitude), eleve ao quadrado cada resultado da variação obtido no passo 2. Isso resulta em valores de variância quadrada que são sempre positivos.
- Some todas as variâncias quadradas: adicione todos os valores de variância quadrada obtidos no passo 3. Esta soma representa a variância total dos pontos de dados em relação à média, ajustada para o tamanho da amostra.
- Divida pelo número de pontos de dados menos um: o próximo passo é dividir a soma das variâncias quadradas pelo número de pontos de dados menos um (n-1). Esta etapa é crucial porque usa um denominador de (n-1) em vez de n, um método conhecido como correção de Bessel, que compensa o fato de que apenas uma amostra da população total está sendo usada e fornece uma estimativa mais precisa da variância da população total.
- Calcule a raiz quadrada do resultado: finalmente, tire a raiz quadrada do quociente obtido na etapa 5. O resultado é o desvio padrão da amostra, que quantifica a quantidade de dispersão ou variabilidade dos pontos de dados em relação à média.
Entender e calcular corretamente o desvio padrão permite aos pesquisadores e analistas fazer inferências mais precisas sobre seus dados e tomar decisões mais informadas.
Como interpretar o desvio padrão?
Interpretar o valor do desvio padrão envolve entender como os dados estão dispersos em relação à média do conjunto de dados. A seguir estão algumas orientações para ajudar na interpretação do desvio padrão:
- Desvio padrão igual a zero: isso significa que todos os valores do conjunto de dados são iguais à média e não há variação. Os dados são perfeitamente uniformes;
- Desvio padrão baixo: um desvio padrão baixo indica que a maioria dos valores do conjunto de dados está próxima da média. Os dados são menos dispersos e estão concentrados em torno da média;
- Desvio padrão alto: um desvio padrão alto sugere que os valores estão mais distantes da média e há uma maior dispersão dos dados.
Para uma interpretação mais concreta, é possível utilizar a regra empírica de 68-95-99,7, que é válida para conjuntos de dados com distribuição normal (ou aproximadamente normal):
- 68% dos valores do conjunto de dados estão dentro de 1 desvio padrão da média (média ± 1 desvio padrão);
- 95% dos valores do conjunto de dados estão dentro de 2 desvios padrão da média (média ± 2 desvios padrão);
- 99,7% dos valores do conjunto de dados estão dentro de 3 desvios padrão da média (média ± 3 desvios padrão).
Lembre-se de que a aplicabilidade dessa regra depende da distribuição dos dados. Se os dados não seguirem uma distribuição normal, a regra pode não se aplicar diretamente. Em geral, o desvio padrão é uma ferramenta útil para compreender a dispersão dos dados, identificar outliers e avaliar a precisão de estimativas estatísticas
5 usos do desvio padrão
Alguns usos comuns são:
1. Medir o risco de investimento
Muitas empresas de investimento utilizam o desvio padrão para determinar o quanto o desempenho do fundo se desvia do retorno normal esperado. Por ser de fácil compreensão, essa estatística pode ser comunicada aos clientes finais e investidores.
Desta forma, o desvio permite avaliar a volatilidade dos valores do mercado e prever tendências futuras de desempenho.
2. Compreender melhor os conjuntos de dados
O desvio padrão é usado para medir a dispersão de valores em um conjunto de dados. O desvio é usado o tempo todo por indivíduos e empresas em diferentes áreas para compreender melhor os conjuntos de dados.
3. Compreender o desempenho do anúncio
Os profissionais de marketing costumam calcular o desvio padrão da receita obtida para cada anúncio para entender qual variação na receita esperar de um determinado anúncio.
Nesta área, o desvio do número de anúncios utilizados pelos concorrentes também pode ser calculado para perceber se utilizam mais ou menos anúncios do que o normal durante um determinado período.
4. Utilização em recursos humanos
Parte do papel do gestor de recursos humanos é calcular o desvio padrão dos salários de uma determinada área para saber que tipo de variação salarial deve oferecer aos novos funcionários.
O desvio padrão é uma ferramenta poderosa para medir dispersão e entender padrões de dados. Seu uso vai desde análises financeiras até gestão de processos e previsão de tendências. Compreender e aplicar corretamente esse conceito é essencial para uma tomada de decisão mais informada e estratégica.





