O Seis Sigma é uma abordagem orientada por dados para a solução de problemas. A abordagem envolve conceitos estatísticos e matemáticos, como a curva de distribuição normal. Os cursos Lean Seis Sigma discutem os principais conceitos estatísticos necessários para resolver problemas de acordo com as regras da metodologia. Os princípios dependem fortemente da compreensão da curva de distribuição normal, conforme discutido brevemente nos cursos gratuitos de Seis Sigma.
Qual é a curva de distribuição normal?
O termo é usado para descrever o conceito matemático chamado distribuição normal, às vezes referido como distribuição Gaussiana ou distribuição de Gauss. Refere-se à forma que é criada quando uma linha é plotada usando os pontos de dados para um item que atende aos critérios de 'Distribuição Normal'.
Como saber se a distribuição é normal?
Existem diferentes métodos para avaliar se uma distribuição é normal ou não. Separamos para você umas dicas para identificar se a curva de distribuição é normal:
- HISTOGRAMA: O histograma é uma ferramenta visual que mostra a frequência dos dados em diferentes faixas de valores. Se a distribuição dos dados se assemelha a uma curva em forma de sino, é um indicativo de que pode ser normal;
- GRÁFICO DE PROBABILIDADE NORMAL: O gráfico de probabilidade normal é um gráfico de dispersão dos dados em relação à distribuição normal teórica. Se os pontos formam uma linha reta, é um indicativo de que a distribuição é normal;
- ESTATÍSTICAS DESCRITIVAS: As estatísticas descritivas, como a média, mediana e desvio padrão, podem fornecer informações sobre a forma da distribuição. Se a média e a mediana são iguais e o desvio padrão é baixo, é um indicativo de que a distribuição é normal.
Quais são as características de uma distribuição normal?
Agora que sabemos identificar uma distribuição Gaussiana, podemos detalhar mais quais são suas características, que, assim como qualquer ferramenta estatística, é extremamente importante para nos ajudar a obter e entender dados. Confira as características dessa tão importante ferramenta:
- Forma de sino: a distribuição é simétrica em torno da média e tem uma forma de sino;
- Média, mediana e moda iguais: a média, mediana e moda estão localizadas no mesmo ponto da distribuição;
- Desvio padrão definido: o desvio padrão define a largura da distribuição e é um indicativo da variabilidade dos dados;
- Área sob a curva: a área total sob a curva é igual a 1, ou seja, a probabilidade de um evento ocorrer é de 100%;
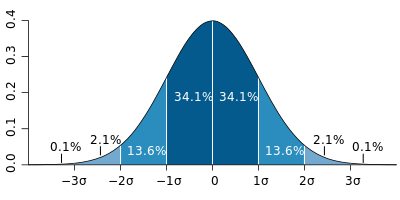
- Regra empírica: a maioria dos dados (cerca de 68%) está localizada dentro de um desvio padrão da média, cerca de 95% dos dados estão dentro de dois desvios padrão da média e quase todos os dados (cerca de 99,7%) estão dentro de três desvios padrão da média;
- Distribuição normal padrão: uma distribuição normal pode ser padronizada com média zero e desvio padrão um, dando origem à distribuição normal padrão.
Fenômenos naturais seguem uma curva de distribuição normal
Muitos fenômenos naturais demonstram um padrão chamado "Curva de Distribuição Normal" ou "Curva de Bell". Se você medir a altura das mulheres em todo o mundo, os resultados seguirão uma forma previsível que se assemelha à forma de um sino.
A temperatura também segue esse padrão. Se você medir a temperatura média do meio-dia nos dias de julho nos EUA a cada ano, você descobrirá que as observações seguiram um padrão de curva de sino.
Você também pode tentar medir a altura de todos os seus colegas no trabalho, ou o tempo que eles levam para tomar uma xícara de café e você encontrará uma curva de distribuição normal padrão.
A estrutura de uma curva de distribuição normal
Vamos ver a estrutura de uma curva de distribuição normal. O centro contém o valor em que o valor do maior número de pontos de dados ocorre e, portanto, seria o ponto mais alto no arco da linha.
Este ponto da curva de distribuição normal é a média ou média. Para usar o exemplo da altura, haverá mais casos de mulheres de altura média do que qualquer outra altura, portanto, o valor da altura média das mulheres no mundo estará no topo da curva de distribuição normal.
A média, mediana e modo de uma curva de distribuição normal
Observe que, no caso de dados distribuídos normalmente, a média será igual à mediana e ao modo . Vamos rever a diferença entre a média, mediana e modo. A média é a soma de todos os valores dos pontos de dados divididos pelo número de pontos de dados.
Se você alinhar todos os valores do menor para o maior, o valor do meio será a mediana. Em contraste, o modo é o número que aparece com mais frequência em um conjunto de pontos de dados. Em uma distribuição normal, a média, a mediana e o modo serão os mesmos.
Outliers em uma distribuição normal
A curva de distribuição normal é concentrada no centro e diminui em ambos os lados. Isso é significativo, pois os dados tendem a ter menos incidências de valores extraordinariamente extremos , chamados outliers ou causas especiais de variação (SCV), em comparação com outras distribuições.
Como o conjunto de dados tem poucos números extremos na extremidade inferior ou superior da escala, a curva achata. Isso é o que dá à curva de distribuição normal sua forma de sino.
Distribuições normais em termos de médias e desvios-padrão
Vamos ver a forma de uma curva de distribuição normal de outro ângulo. Um gráfico de curva de distribuição normal depende de dois fatores, a média e o desvio padrão. Vamos rever rapidamente a definição de desvio padrão.
O desvio padrão é uma medida de quão estreitamente agrupado ou quão espaçado aparece um conjunto de dados. É uma das medidas de dispersão. Uma distribuição normal padrão tem uma média de zero e um desvio padrão de um. A média identifica a posição do centro e o desvio padrão determina a altura e largura do sino.
Por exemplo, um grande desvio padrão cria uma campainha plana e larga, enquanto um pequeno desvio padrão cria uma curva estreita e mais íngreme. A regra é simples. Quanto mais plana a curva, maior a variação. Quanto mais íngreme a curva, menor a variação.
Um exemplo prático para curva de distribuição normal
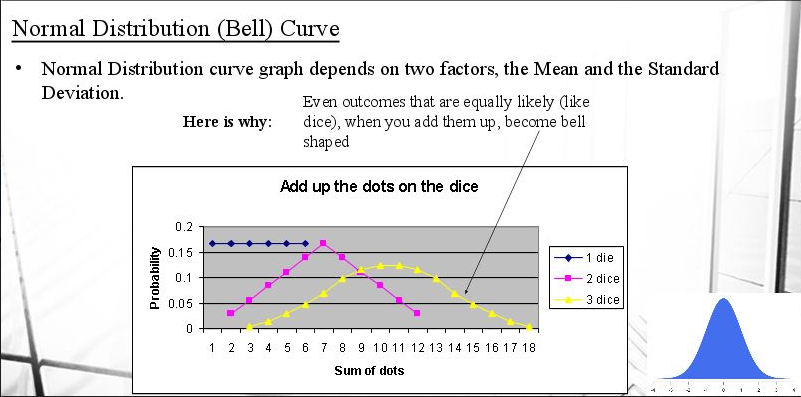
Veja o exemplo abaixo:
- Se você rolar um único dado, a possibilidade de cada número ser rolado é em torno de 16,67% para cada número.
- Se você rolar dois dados, a possibilidade da soma dos pontos será como mostrado na linha rosa. Será de 2 a 12, respectivamente. Mas, como você vê, a possibilidade de obter a soma de 7 é a mais alta, que é na verdade 2 mais 12 dividido por 2.
- Finalmente, se você rolar três dados ao mesmo tempo, a possibilidade da soma dos pontos será mostrada na linha amarela. O resultado será de 3 a 18. Mas, como você vê, a possibilidade de obter a soma de 10 ou 11 é a mais alta, que é na verdade próxima a 10,5 e isso se for encontrado por 3 mais 18 dividido por 2.
Agora, vamos também lembrar a regra empírica do desvio padrão. Diz que dentro de uma distribuição normal padrão:
- 68% dos pontos de dados estarão dentro de ± um desvio padrão da média
- 95% estarão dentro de ± dois desvios padrão
- 99,73% dos pontos de dados estarão dentro de ± três desvios-padrão da média
A curva de distribuição normal é uma distribuição de probabilidade em que o valor que ocorre com mais frequência está no meio e outras probabilidades se afastam simetricamente em ambas as direções.
- Teoricamente não atinge zero
- Pode ser dividida ao meio, com valores iguais em ambos os lados Do valor mais frequente
- Indica variação aleatória ou aleatória
- O pico da curva representa o centro do processo
- São divididas em 3 desvios padrão em cada lado da média
Resumo
A curva é um dos conceitos estatísticos mais importantes do Lean Seis Sigma. Resolve problemas onde o número de defeitos é muito alto. Um alto número de defeitos é estatisticamente igual a alta variação no processo.
Visualiza a variação em um conjunto de dados. O conjunto de dados representado pela curva de distribuição normal pode se referir ao tempo de inatividade na fabricação ou ao tempo necessário para atender uma chamada em um call center.
Se os dados seguem uma curva de distribuição normal, isso significa que os dados são elegíveis para determinados testes estatísticos que são usados no estágio de análise do processo Seis Sigma. Dica: a certificação Green Belt visa capacitar profissionais das mais diversas áreas de atuação na otimização de processos utilizando a metodologia Lean Seis Sigma.