Como surgiram os Gráficos de Controle?
Atribui-se ao Dr. Walter A. Shewhart, considerado o pai do controle estatístico de qualidade, o desenvolvimento do gráfico de controle (ASQC, 1976). Em 1924, Shewhart anexou um gráfico a um memorando direcionado ao Diretor de Engenharia de Inspeção do Laboratório da Bell Telephone. O memorando respondia a um pedido para:
“... o desenvolvimento de uma forma aceitável de relatório de inspeção que possa ser modificado de tempos em tempos, a fim de fornecer à primeira vista a maior quantidade de informação precisa.”
Shewhart foi bem além do pedido original. Ele publicou os detalhes do método do gráfico de controle no Bell System Technical Journal de 1926 a 1930. Em 1931, Shewhart publicou o livro Economic Control of Quality of Manufactured Product, o qual inclui a teoria e a aplicação de gráficos de controles. Estes são chamados de gráficos de Shewhart em algumas partes do mundo para distinguir gráficos baseados na teoria de Shewhart de outros gráficos de “controle”. A predição era o conceito chave na definição de “controle” (Shewhart, 1931, p. 6):
“Um fenômeno é dito controlado quando, por meio do uso da experiência passada, pudermos prever, pelo menos dentro de limites, como se pode esperar que o fenômeno varie no futuro.”
Por meio de seu trabalho na Western Electric, Shewhart descobriu que características de qualidade em processos de manufatura tendem a não estar em controle. Ele também descobriu que era possível identificar e remover as causas de situações fora de controle e trazer o processo para um estado de controle. Tudo sobre Gráfico de Controle, você fica sabendo em nossa Certificação Green Belt e Black Belt.
O que é um Gráfico de Controle?
O gráfico de controle consiste em três linhas plotadas em um gráfico construído, obtendo-se medidas para algumas características de um processo. Os dados são então agrupados pelo período de tempo, local ou outras variáveis descritivas. Esses conjuntos de dados são chamados de subgrupos, que são obtidos com frequência ao longo do tempo e que são necessários para se construir um gráfico de controle.
[caption id="attachment_9225" align="aligncenter" width="577"]
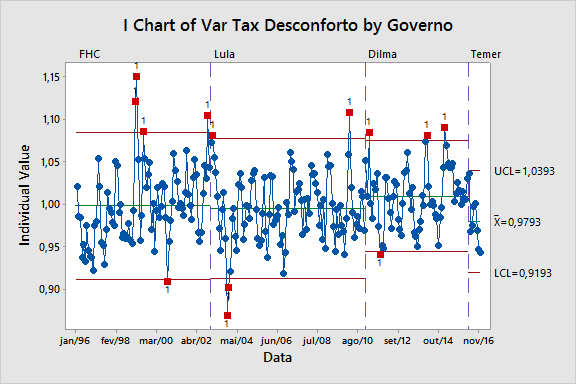Figura 1: Exemplo de Gráfico de Controle[/caption]Uma estatística descritiva, tais como média, amplitude ou percentual com defeito, é calculada a partir das medidas em cada subgrupo. A estatística é então plotada em um gráfico com o eixo horizontal, sendo o número do subgrupo e o eixo vertical sendo a escala para a estatística.
Quando 20 a 30 subgrupos forem plotados no gráfico, os limites de controle podem ser calculados. Estes limitam a variação da característica de qualidade devido a causas comuns, sendo que foram desenvolvidas fórmulas para os limites de controle para todos os tipos comuns de gráficos de controle. Apesar dos limites serem baseados na teoria estatística, Deming (1986) diz claramente que os limites de controle não devem ser associados com qualquer cálculo de probabilidade.
Ao desenvolver o método do gráfico de controle, Shewhart enfatizou a importância do equilíbrio econômico entre procurar causas especiais que não existem e deixar de lado causas que de fato existem. Foi também necessário desenvolver regras que deem um equilíbrio econômico aceitável para todos os tipos de medidas em uma variedade de sistemas, processos e produtos.
Por que os limites de controle são três sigmas (desvios padrão)?
As razões fundamentais para o uso dos limites de três sigmas de Shewhart são:
- Os limites têm base na teoria estatística;
- Os limites provaram na prática que distinguem causas especiais de causas comuns de variação;
- Na maior parte dos casos, o uso de limites minimizará o custo total devido tanto à reação excessiva quanto à falta de reação à variação no processo;
- Os limites protegem a moral dos trabalhadores no processo ao definir a magnitude da variação que está embutida no processo.
O que é um subgrupo no gráfico de controle?
O conceito de subgrupo é um dos mais importantes componentes do método de gráfico de controle. Shewhart disse o seguinte a respeito da construção dos subgrupos:
“Obviamente, o objetivo final é não apenas detectar problemas, mas também encontrá-los, e tal descoberta naturalmente envolve classificação. O engenheiro que é bem-sucedido em dividir seus dados em subgrupos racionais baseado em hipóteses racionais está, portanto, inerentemente melhor no longo prazo do que um que não seja assim tão bem-sucedido.” (Shewhart, 1931, p.229)
O conceito de Shewhart é o de organizar (classificar, estratificar, agrupar etc.) os dados dos processos de um modo que provavelmente faça com que os dados de cada subgrupo tenham as maiores chances de serem parecidos e que os dados de outros grupos tenham as maiores chances de serem diferentes. O propósito do subgrupamento racional é o de incluir apenas causas comuns de variação dentro de um subgrupo, com todas as causas especiais de variação ocorrendo entre subgrupos.
O que é a estratificação no gráfico de controle?
A estratificação é a separação e a classificação de dados de acordo com variáveis ou fatores selecionados, tendo como objetivo encontrar padrões que ajudem a entender os mecanismos causais em um processo. A estratificação em um gráfico de controle está usualmente focalizada no ordenamento dos subgrupos, com ordem de tempo mais prevalecente. Os subgrupos podem também ser ordenados por outros fatores tais como fornecedor, turno, operador, posição da peça etc., para investigar a importância desses fatores.
Como eu escolho os subgrupos do meu gráfico de controle?
O método mais comum de se obter subgrupos racionais é o de manter o tempo “constante” dentro de um subgrupo. Apenas dados obtidos no mesmo tempo, ou para algum período de tempo selecionado, são incluídos em um subgrupo. Dados de períodos de tempo diferentes estarão em outros subgrupos. Esse uso do tempo como base do subgrupamento permite a detecção de causas de variação que vêm e vão com o tempo.
Como exemplo de subgrupamento, considere um estudo planejado para reduzir pagamentos atrasados. Os dados históricos dos arquivos de contabilidade serão usados para estudar a variação no assunto. O que é uma boa maneira de se subgrupar os dados históricos sobre pagamentos atrasados?
Os dados podem ser agrupados por mês de vencimento, mês de recebimento, por conta principal, por linha de produto ou por gerente de conta. Conhecimento ou teorias a respeito do processo devem ser usados para desenvolver subgrupos racionais. Algumas combinações de tempo (mês de recebimento ou de vencimento) e uma ou mais das outras variáveis no processo seriam um modo razoável de se desenvolver o primeiro gráfico de controle.
Após selecionar o método de subgrupamento, o usuário do gráfico de controle deve ser capaz de dizer quais fontes de variação no processo estarão presentes dentro de subgrupos e quais fontes ocorrerão entre subgrupos. O objetivo específico do gráfico de controle com frequência ajudará a determinar a estratégia para o subgrupamento dos dados. Por exemplo, se o objetivo for o de avaliar diferenças entre fornecedores de matéria prima, então apenas matérias de um único fornecedor devem ser incluídas nos dados de cada subgrupo.
Quais são os tipos de gráfico de controle?
O gráfico apropriado para se usar em uma aplicação particular depende primariamente do tipo dos dados.
- Para dados de classificação, a característica de qualidade é registrada em uma de duas classes. Exemplos dessas classes são unidades conformes/não conformes, tolerável/não tolerável ou bom/ruim.
- Para se obter dados de contagem, os números de incidências de um tipo particular são registrados: número de erros, número de acidentes ou número de indicações de vendas.
- Para dados contínuos é registrado o valor numérico medido da característica de qualidade, por exemplo uma dimensão, atributo físico ou número calculado.
Deve-se notar que dados para algumas características de qualidade podem ser registrados como qualquer um dos três tipos. Por exemplo, para algo com um grande número de características dimensionais, os dados podem ser registrados em qualquer uma das seguintes maneiras:
- classificação: o objeto atende ou não às especificações;
- contagem: número de dimensões que não atendem a especificações;
- contínua: valor medido para as dimensões selecionadas.
Dados contínuos podem ser convertidos para dados de atributo aplicando-se uma definição operacional para a contagem ou classificação. Uma dimensão registrada pode ser classificada como atendendo ou não à especificação, entretanto, essa conversão não funciona na outra direção. As dimensões medidas são desconhecidas para um objeto que é registrado como não atendendo às especificações.
De um modo geral, sempre que possível os dados devem ser coletados como dados de variáveis, já que o aprendizado pode ocorrer com muito menos medidas se comparado com as classificações ou contagens de atributos.
Os gráficos de controle para dados de variáveis requerem menos medidas em cada subgrupo do que o gráfico de controle de atributo. Os tamanhos de subgrupos típicos para gráficos de dados de variáveis variam de 1 a 10, enquanto que os tamanhos de subgrupo para dados de atributo variam de 30 a 1000.
Como saber qual gráfico utilizar?
A Figura 2 contém um resumo de gráficos frequentemente usados e o tipo de dados aos quais eles se aplicam. Para dados contínuos, duas estatísticas descritivas importantes das medidas em um subgrupo são a média das medidas e a amplitude (maior medida menos a menor medida). A média é chamada de X-barra e a amplitude de R. Dois gráficos de controle são necessários: o gráfico de X-barra para as médias e o gráfico R para as amplitudes. São incluídas de duas a dez medidas para cada subgrupo, e os tamanhos mais comuns de subgrupos variam de três a seis.
[caption id="" align="aligncenter" width="547"]
Figura 2: Tipos de gráficos de controle[/caption]E se o tamanho do subgrupo for variável?
Se o tamanho do subgrupo for variável (o número de medidas muda de um subgrupo para outro), o desvio padrão (outra estatística descritiva para a variação) é usada no lugar da amplitude. Os gráficos X-barra e S são usados nesse caso, no qual S é o símbolo para o desvio padrão dos valores no subgrupo. Para a maior parte das aplicações com dados de variáveis, o tamanho do subgrupo pode ser mantido constante. Assim, o gráfico S tem uso limitado.
Em algumas aplicações não é prático ter medidas múltiplas em um subgrupo. Por exemplo, existe apenas uma determinação do número mensal de vendas. Nessas aplicações, a medida única é tratada como um subgrupo e é plotada em um gráfico X.
Quando as unidades de amostragem são classificadas em duas categorias (unidades conformes e não conformes), o gráfico P (p = porcentagem não conforme) é apropriado. O gráfico P pode ser usado tanto com um tamanho de subgrupo fixo quanto variável. O gráfico NP (np = número de unidades não conformes) só pode ser usado quando o tamanho do subgrupo é constante.
Para dados de contagem, o gráfico C (número de incidências) é apropriado quando a oportunidade para uma ocorrência é relativamente constante em cada subgrupo. O gráfico U (número de incidências por unidade) é necessário para dados de contagem quando a oportunidade para a ocorrência é variável entre subgrupos. O tamanho do subgrupo é substituído pelo conceito de área de oportunidade para os gráficos C e U.
Há outros tipos de gráficos de controle, tais como o gráfico de controle da mediana e o gráfico de soma cumulativa, usados para aplicações especiais. Os sete tipos de gráficos mostrados na Figura 2 são os gráficos de controle de Shewhart mais encontrados na prática.
Para entender mais sobre o assunto, você pode realizar o nosso curso grátis de White Belt, em que explicamos mais detalhadamente o tema.
