A Regressão Linear é uma técnica estatística amplamente utilizada na área de gestão de projetos para prever resultados futuros com base em dados históricos. Ela permite entender a relação entre duas ou mais variáveis e utilizar essa informação para tomar decisões informadas
Neste artigo, nós iremos explorar toda a teoria por trás da regressão linear e mostrar como ela pode ser fundamental na sua organização.
O que é Regressão Linear e para que serve?
A regressão linear é baseada na hipótese de que existe uma relação linear entre as variáveis dependentes e independentes. Isso significa que o aumento ou a diminuição de uma variável independente leva a um aumento ou a uma diminuição proporcional na variável dependente. A regressão linear é capaz de determinar a magnitude e a direção desta relação.
A regressão linear é geralmente realizada utilizando o método de mínimos quadrados, que busca encontrar a linha de melhor ajuste para os dados. Esta linha de melhor ajuste é conhecida como a equação da reta da regressão linear. A partir desta equação, é possível realizar previsões sobre a variável dependente com base nos valores das variáveis independentes.
Como utilizar a regressão linear?
Será que todos vão ficar acima do peso ou se tornar obesos? Sim, segundo um artigo que li: por volta de 2048, todos os americanos já estarão obesos. Se eu fosse americano, em 2048 teria 64 anos e esperaria não ser obeso, mas li que seria. O que fazer?
Esse artigo da Obesity teve muita publicidade. Vários jornais alertaram para o “apocalipse da obesidade”, que “todos estamos mais gordos” e coisas do gênero. Ellenberg, no entanto, lembra que esse tipo de reação é muito comum nos EUA: no pós-guerra, por exemplo, quando rapazes deixavam crescer o cabelo, passam a estar sujeitos a serem açoitados pelos comunistas.
Já em nossa geração, quem joga videogame demais está fadado a sair matando de maneira indiscriminada por pura diversão e, agora, comeremos fast-food demais e todos morreremos fracos e imóveis, cercados de embalagens de papelão vazias, estirados em sofás dos quais há muito perdemos a capacidade de nos levantar. O artigo sobre obesidade certificava essa ansiedade comum a todos nós como um fato cientificamente comprovado. Mas...
Não estamos fadados a ficar acima do peso em 2048. Por quê? Porque nem toda curva é uma reta – mas, como já dizia Newton, toda curva é bem próxima de uma reta. Essa é a ideia que orienta a regressão linear, técnica estatística que está para as ciências sociais como a chave de fenda para os consertos domésticos. É aquela ferramenta que você vai usar quase com certeza, qualquer que seja o serviço.
Toda vez que você lê no jornal que pessoas com mais primos são mais felizes, ou que países com mais fast-foods têm preceitos morais mais amplos, ou que cortar pela metade o consumo de vitamina B3 duplica o risco de ter pé de atleta, ou que a cada US$ 10 mil a mais em renda tornam alguém 3% mais propenso a tornar-se de direita, você está encontrando o resultado de uma regressão linear.
Por que a regressão linear é importante?
A regressão linear é importante porque é uma técnica amplamente utilizada em estatística e análise de dados para modelar a relação entre uma variável dependente e uma ou mais variáveis independentes. É uma ferramenta útil para fazer previsões sobre uma variável de interesse a partir de dados históricos e para entender como diferentes variáveis estão relacionadas entre si. Além disso, a regressão linear é simples e fácil de implementar, tornando-a uma escolha popular para muitos problemas de análise de dados.
Exemplo da utilização da regressão linear
Você tem duas coisas que quer relacionar – digamos, o custo de anuidades da universidade e a média de resultados dos exames finais do ensino médio dos alunos admitidos. Você poderia pensar que as universidades cujos alunos tiveram resultados mais elevados teriam propensão a ser mais caras. No entanto, uma olhada nos dados nos diz que essa não é uma lei universal.
A Elon University tem uma pontuação média de 1.217 e cobra uma anuidade de 20.441,00; já o Guilford College, enquanto cobra 23.420,00, tem como pontuação média nos exames de conclusão para ingresso apenas 1.131. Se você observar as 31 universidades privadas que informaram suas anuidades e pontuações para ingresso em 2007, perceberá uma tendência clara.
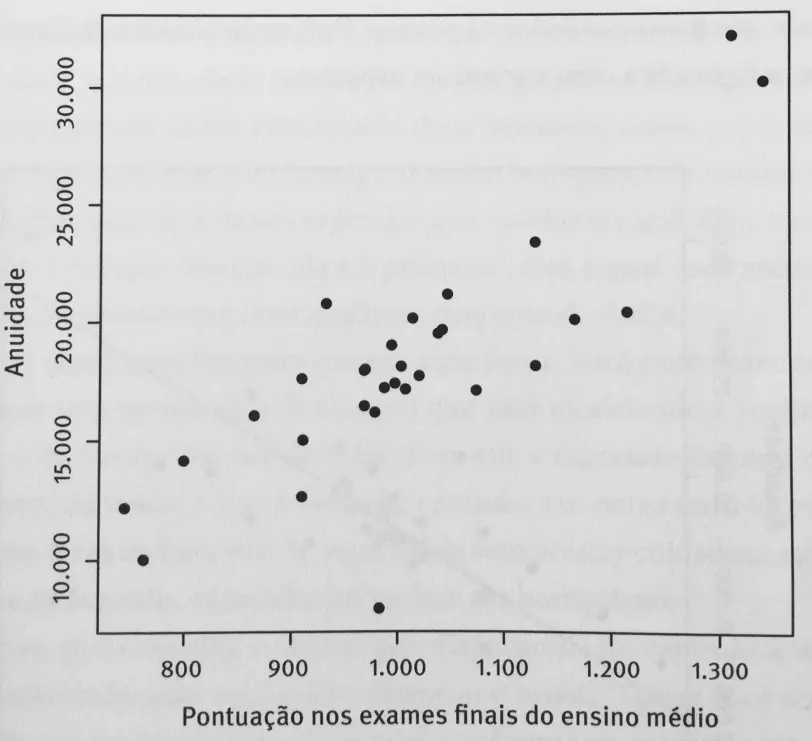
Figura 1: gráfico de dispersão entre anuidade e pontuação nos exames finais do EM.[
Cada ponto do gráfico representa uma das faculdades. Os dois pontos bem altos no canto superior direito, com pontuações de exames e preços nas alturas, correspondem à Wake Forest e à Davidson; e o ponto solitário perto da base, a única escola privada na lista com anuidade inferior a 10 mil, representa a Cabarrus College.
A figura 1 mostra claramente que universidades com notas mais altas têm, em geral, preços mais altos. Porém, quanto? É aqui que a regressão linear entra em cena. Os pontos da figura não estão obviamente numa linha reta.
Provavelmente você poderia traçar uma linha reta a mão livre cortando muito aproximadamente o meio dessa nuvem de pontos, mas é nesse momento que entra em ação a regressão linear, expulsando o trabalho de adivinhação e revelando a reta que mais se aproxima de passar por todos os pontos.
Como encontrar a "reta da previsão" na regressão linear?
Para encontrar o que significa “mais se aproxima”, deve-se: substituir a anuidade real de cada escola pela estimativa sugerida pela reta e então computar a diferença entre a anuidade real e a estimada para cada escola; em seguida deve-se elevar ao quadrado cada um desses números e por fim somar todos esses quadrados.
Aí você obterá uma espécie de medida total de quanto a reta está desviada em relação aos pontos, podendo escolher a que torna essa medida a menor possível. Quadrados? Pitágoras?
A geometria subjacente à regressão linear nada mais é que o teorema de Pitágoras transposto e alçado a um contexto dimensional muito mais elevado, só que essa história requer mais álgebra do que nos interessa neste momento.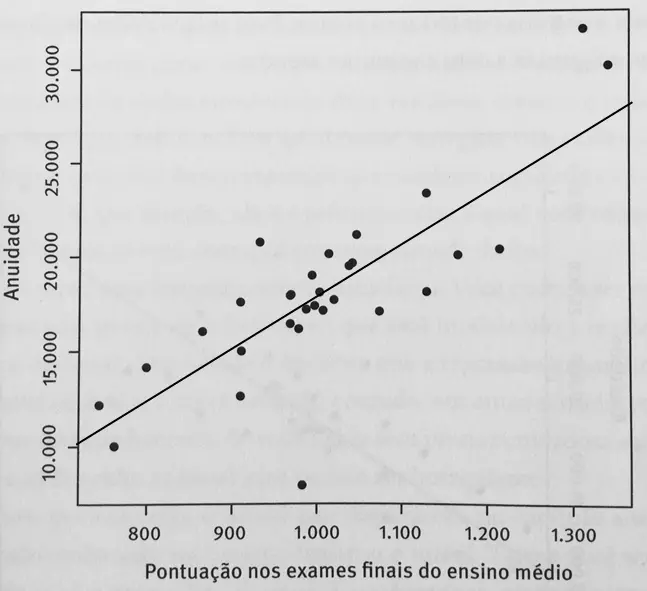
Figura 2: regressão linear entre anuidade e pontuação nos exames finais do EM.
A reta na figura 2 tem uma inclinação de cerca de 28º. Isso significa que se a anuidade fosse de fato totalmente determinada pela pontuação dos exames finais, cada ponto extra nos exames corresponderia a 28 dólares a mais na anuidade.
Se você, como universidade, puder aumentar a média nos exames dos seus calouros admitidos em cinquenta pontos, poderá cobrar US$ 1.400 a mais de anuidade; enquanto que, pela visão dos pais, cem pontos do filho irão custar US$ 2.800 a mais por ano.
A regressão linear é uma ferramenta maravilhosa, escalável e tão fácil de executar quanto clicar um botão na sua planilha. Você pode usá-la para conjuntos de dados envolvendo duas variáveis, como no exemplo anterior, mas funciona igualmente bem para três variáveis, ou mil.
Sempre que você desejar entender que variáveis conduzem a outras variáveis, e em que direção, ela é a primeira coisa à qual você recorre. E funciona absolutamente com qualquer conjunto de dados.
Quais cuidados tomar na hora de fazer uma regressão linear?
- Verificação de linearidade: é importante verificar se existe uma relação linear entre as variáveis independentes e a variável dependente.
- Tratamento de outliers: outliers podem afetar significativamente o modelo de regressão linear, portanto, é importante identificá-los e decidir como lidar com eles.
- Verificação de multicolinealidade: se duas ou mais variáveis independentes são altamente correlacionadas, isso pode afetar negativamente o modelo de regressão linear.
- Verificação de normalidade: é importante verificar se a distribuição dos resíduos é normal, pois isso é uma suposição importante da regressão linear.
- Seleção de variáveis: é importante escolher as variáveis independentes apropriadas para incluir no modelo, o que pode ser feito por meio de métodos estatísticos.
- Validação do modelo: é importante validar o modelo de regressão linear utilizando dados de teste ou dados independentes para avaliar a capacidade de previsão do modelo.
A regressão linear em um míssil
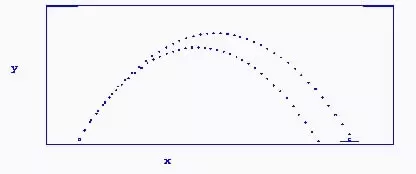
Figura 3: trajetória do lançamento de um míssil ICBM.
Imagine que a figura 3 seja um registro das posições de um míssil em momentos distintos. Animado pelo novo conceito que aprendeu, você faz uma rápida regressão linear e obtém ótimos resultados: uma reta que passa quase exatamente pelos pontos que você registrou
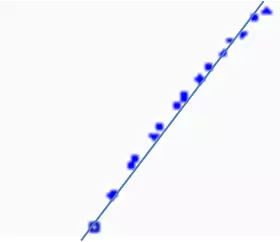
Figura 4: linha reta que passa pela trajetória do míssil.
Sua reta fornece um modelo muito preciso para o movimento do míssil: para cada minuto que passa, o míssil aumenta sua altitude num valor fixo de 400 metros. Após uma hora, por exemplo, estará a 24 quilômetros de altitude.
Mas quando é que ele desce? Não desce nunca: uma reta inclinada ascendente segue seu rumo indefinidamente. E agora? É um novo míssil espião alienígena?
É válido frisar que nem toda curva é uma reta – como é o caso da curva do voo do míssil, que na verdade é uma parábola. Lembra-se das aulas de física do colegial? Trata-se de movimento balístico, não é mesmo?
Exatamente como o círculo de Arquimedes, ela parece uma reta quando vista de perto e é por isso que a regressão linear faz um bom serviço dizendo-lhe onde o míssil estará cinco segundos depois que você o rastreou da última vez. Mas e uma hora depois? Seu modelo dirá que o míssil está na estratosfera, passeando pelo espaço sideral.
Ellenberg cita um trecho de Vida no Mississipi, de Mark Twain, para mostrar o perigo da extrapolação linear impensada.
“O Mississipi entre o Cairo e Nova Orleans tinha 1.960 quilômetros de comprimento 176 anos atrás. Passou a ter 1.900 após o corte de 1722. Tinha 1.670 após o corte American Bend. Desde então perdeu 123 quilômetros. Consequentemente, seu comprimento é de apenas 1.547 quilômetro no presente. ... No espaço de 176 anos, o baixo Mississipi encolheu 399 km. É uma média de mais de 2 km por ano.
Portanto, qualquer pessoa calma, que não seja cega ou idiota, poder ver que, no período oolítico siluriano, pouco mais de 1 milhão de anos atrás, o baixo rio Mississipi tinha mais de 2 milhões de quilômetros de comprimento, estendendo-se sobre o golfo do México como uma vara de pescar.
Do mesmo modo, qualquer pessoa pode ver que daqui a 742 anos o baixo Mississipi terá apenas 2 km de comprimento, e Cairo e Nova Orleans terão juntado suas ruas e estarão labutando confortavelmente juntas sob um único prefeito e um conselho de anciãos. Há algo fascinante na ciência. Obtemos tais retornos de conjectura por atacado a partir de uma ninharia de investimento de fato.”
Como a regressão linear te ajuda a emagrecer?
Qual o percentual de americanos que estarão acima do peso em 2048? Como será que o grande autor Youfa Wang e seus colaboradores geraram essa projeção para o artigo da revista Obesity? Observemos que o Estudo Nacional do Exame sobre Saúde e Nutrição, instituição que acompanha o índice de massa corporal (IMC), classifica como acima do peso pessoas com IMC maiores de 25.
Segundo seus dados, no começo dos anos 1970 pouco menos da metade dos americanos tinham IMC tão alto, mas no começo dos anos 1990 esse número já era quase 60% e em 2008, próximo a 75%.
Gerando a regressão linear desses dados – e os extrapolando -, essa reta cruzaria 100% em 2048 e é por isso que Wang afirma que, se a tendência atual continuar, todos os americanos serão obesos.
Mas é claro que a tendência não vai continuar, pois é impossível que em 2060 109% dos americanos sejam obesos. Dessa forma, podemos concluir que, assim como a gravidade transforma a trajetória inicialmente reta do míssil em uma parábola, o que a princípio parecia uma lei também pode se alterar.
Quanto maior a proporção de pessoas acima do peso, menos magros restam para converter e mais lentamente a proporção aumenta em direção aos 100%. Na verdade, a curva provavelmente vai se tornar horizontal em algum ponto abaixo dos 100%: sempre haverá magros entre nós.
De fato, apenas quatro anos depois o levantamento do Centro de Saúde mostrou que a escalada do predomínio do sobrepeso já havia começado a desacelerar.
Quais os erros possíveis da regressão linear?
O artigo sobre a Obesity oculta o PIOR CRIME contra a matemática e o senso comum. A regressão linear é fácil de fazer – uma vez que se fez uma, as outras são tranquilas. Wang e companhia, então, dividiram seus dados segundo grupos étnicos e sexo.
Homens negros, por exemplo, tinham menos propensão a estar mais acima do peso que o americano médio, e, mais importante, sua taxa de sobrepeso crescia apenas com metade da velocidade.
Se sobrepusermos a proporção de homens negros acima do peso à proporção global de americanos acima do peso, juntamente com a regressão linear que Wang e companhia elaboraram, veremos que homens negros são mais magros: eles só estariam todos acima do peso em 2095, sendo que em 2048, só 80% seriam obesos.
Conseguem localizar o problema? Se todos os americanos estarão acima do peso em 2048, onde deverá estar aquele 1 em 5 futuros homens negros sem problema de peso? No exterior?
A contradição básica passa sem ser mencionada no artigo, fazendo-me lembrar das brincadeiras que fazíamos na escola quando algum colega, numa prova de física, registrava que a altura do poste era de 5 quilômetros.
Lembre-se: higiene matemática é importante. Quando estiver testando um método matemático em campo, tente computar a mesma coisa de várias maneiras diferentes: se obtiver respostas diferentes, há algo de errado em seu método.
