Você já ouviu falar em intervalo de confiança? Esse conceito estatístico está presente em pesquisas eleitorais, controle de qualidade na indústria e até na análise de investimentos. Mas será que você sabe realmente o que ele significa e como interpretá-lo corretamente?
Neste artigo, vamos explicar o que é um intervalo de confiança, como calculá-lo e onde ele é aplicado na prática. Você entenderá por que um intervalo mais estreito significa mais precisão, como erros comuns podem levar a interpretações equivocadas e de que forma esse conceito pode impactar decisões importantes no seu dia a dia.
O que é intervalo de confiança?
O intervalo de confiança indica a faixa em que um parâmetro populacional provavelmente se encontra. Em estatística, ele representa a incerteza associada a uma estimativa. Quanto maior o intervalo, maior a variabilidade da amostra.
A base desse conceito está na inferência estatística, que utiliza amostras para fazer previsões sobre um grupo maior. O intervalo de confiança é sempre acompanhado de um percentual, como 90%, 95% ou 99%, que indica a probabilidade de o verdadeiro valor estar dentro desse intervalo.
Relação com a margem de erro
A margem de erro define o quanto uma estimativa pode variar dentro do intervalo de confiança. Se uma pesquisa aponta que um candidato tem 40% das intenções de voto, com uma margem de erro de 3 pontos percentuais, o intervalo seria de 37% a 43%.
Quanto menor a margem de erro, mais precisa é a estimativa. Isso depende do tamanho da amostra e da variabilidade dos dados. Amostras maiores tendem a reduzir essa margem, tornando o intervalo mais estreito.
Diferença entre intervalo de confiança e nível de significância
Certamente você já deve ter se confundido com ambos os nomes, então vamos tirar essas dúvidas. Quando falamos em nível de significância ela serve para complementar o intervalo de confiança. Se o intervalo tem 95% de confiança, significa que há 5% de chance de erro na estimativa. Esse percentual de erro é chamado de nível de significância.
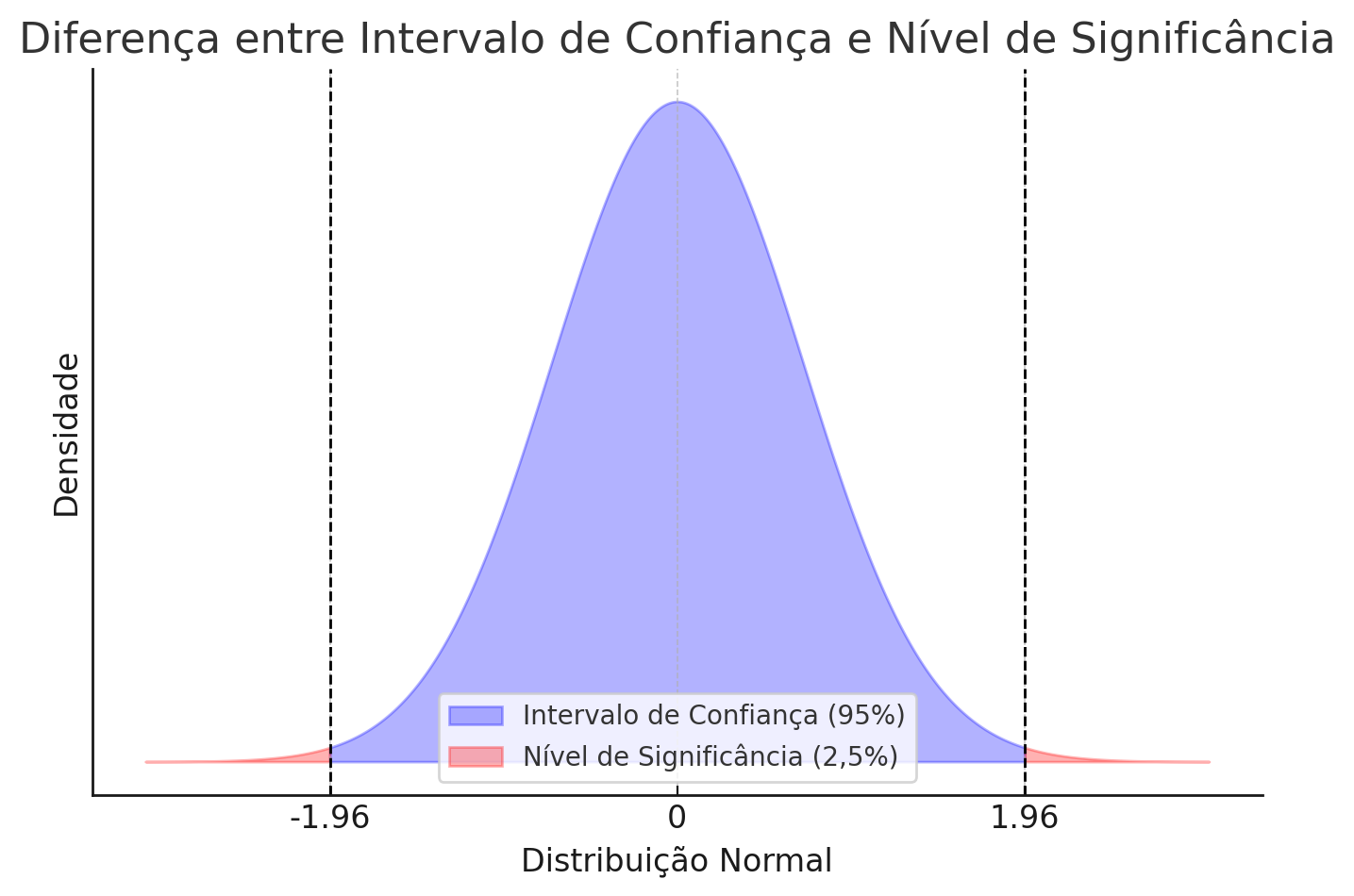
No gráfico a área central em azul, representa o intervalo de confiança de 95%, que abrange o valor do parâmetro tem alta probabilidade de estar. Já a área vermelha representa o nível de significância de 5% (2,5% em cada extremidade), que indica a chance de erro ao rejeitar uma hipótese verdadeira.
Colocando para um exemplo prático, um supervisor que atua na parte de controle de qualidade de uma fábrica de refrigerantes deseja garantir que cada garrafa contenha 1,0 litro do produto. Após realização de testes, encontraram um intervalo de confiança de 95% entre 0,98 litros e 1,02 litros. Isso significa que há 95% de chance de o volume médio real estar dentro desse intervalo.
O valor do nível de significância ser de 5% indica que há 5% de risco de o volume médio real ser menor que 0,98 L ou maior que 1,02 litros.
Como interpretar um intervalo de confiança?
O que significa um intervalo de confiança de 95%?
Seguindo o exemplo anterior, um intervalo de confiança de 95% utilizado no controle de qualidade da fábrica de refrigerantes indica que, se várias amostras (garrafas) forem coletadas e analisadas, em 95% dos casos o verdadeiro valor populacional estará dentro do intervalo calculado.
Isso não significa que o intervalo cobre 95% dos dados ou que há 95% de certeza sobre um único intervalo. Em vez disso, reflete a confiabilidade da estimativa ao longo de múltiplas repetições do estudo.
Se naquela fábrica de refrigerante encontra um intervalo de confiança de 0,98L a 1,02L, há 95% de chance de o volume médio real do lote estar dentro desse intervalo.
Intervalos mais largos e mais estreitos: impacto na precisão
O tamanho do intervalo de confiança está ligado à precisão da estimativa.
- Intervalos mais largos indicam maior incerteza, tornando a previsão menos útil.
- Intervalos mais estreitos fornecem maior precisão, mas exigem amostras maiores ou menor variabilidade nos dados.
No exemplo da fábrica de refrigerantes, onde o controle de qualidade mede o volume para garantir que contenham 1,0 litro do produto. Se a análise resultasse em um intervalo de confiança de 95% entre 0,95L e 1,05L, isso indica maior incerteza. O volume médio real pode estar em qualquer ponto desse intervalo, mas a variação é grande. Esse intervalo mais largo pode sugerir inconsistências no processo de envase.
Agora, se o intervalo for 0,99L a 1,01L, a precisão é maior. A incerteza diminui, pois o volume real das garrafas está mais próximo de 1,0L. Um intervalo mais estreito indica um controle de qualidade mais eficiente e um processo de envase mais estável.
Se a fábrica quiser reduzir o intervalo, pode aumentar o tamanho da amostra ou melhorar a precisão das máquinas de envase.
Erros comuns na interpretação
Saber interpretar o resultado faz parte de como conseguir solucionar os problemas e propor melhorias dentro do ambiente de trabalho, por isso listamos 3 pontos importantes que as pessoas costumam errar.
- Achar que o intervalo cobre 95% dos dados individuais: O intervalo de confiança se aplica ao parâmetro populacional, não aos valores individuais das amostras.
- Acreditar que há 95% de certeza sobre um único intervalo: O percentual se refere a múltiplas amostras, não a um único cálculo.
- Ignorar a influência do tamanho da amostra: Amostras pequenas aumentam a variação e podem gerar intervalos menos confiáveis.
Quer entender melhor como garantir processos mais confiáveis na sua empresa? Aprenda com o curso Fundamentos da Gestão da Qualidade gratuitamente.

Como calcular o intervalo de confiança?
1. Fórmula geral do intervalo de confiança
O intervalo de confiança é calculado usando a seguinte fórmula:
IC=xˉ±(Z×EP)
Onde:
- xˉ (média amostral): Representa a média dos valores coletados na amostra.
- Z: Valor crítico da distribuição normal (ou t da distribuição t-Student) correspondente ao nível de confiança.
- EP (erro padrão): Mede a variabilidade da média da amostra em relação à população.
Essa fórmula fornece os limites inferior e superior dentro dos quais o parâmetro populacional deve estar com uma determinada confiança.
2. Passo a passo do cálculo
Definição do nível de confiança
O primeiro passo é escolher o nível de confiança, que indica a probabilidade de o verdadeiro valor populacional estar dentro do intervalo. Os mais comuns são:
- 90% → Z = 1,645
- 95% → Z = 1,96
- 99% → Z = 2,576
Cálculo do erro padrão
O erro padrão (EP) é obtido pela fórmula:
EP=σ\√n
Onde:
- σ: desvio padrão da população (ou da amostra, caso a população seja desconhecida).
- n: tamanho da amostra.
Amostras menores tendem a ter maior erro padrão, resultando em intervalos de confiança mais amplos.
Uso da distribuição normal e t-Student
- Quando a amostra é grande (n>30), usa-se a distribuição normal (Z), assumindo que a população segue uma distribuição normal ou a amostra obedece ao Teorema do Limite Central.
- Quando a amostra é pequena (n≤30) e o desvio padrão populacional é desconhecido, usa-se a distribuição t-Student, que ajusta a incerteza pela variabilidade da amostra.
3. Diferença entre amostras grandes e pequenas
Quando usar a distribuição normal (Z)?
Se o tamanho da amostra for maior que 30, e a população seguir uma distribuição normal, a distribuição Z pode ser utilizada. Ela é mais precisa para dados que já possuem pouca variabilidade.
Quando usar a distribuição t-Student?
Se a amostra for menor que 30, e o desvio padrão da população for desconhecido, a distribuição t-Student deve ser usada. O valor de t depende dos graus de liberdade (n−1), o que torna o intervalo mais amplo do que na distribuição normal.
Exemplos práticos de intervalo de confiança
1. Intervalo de confiança em pesquisas estatísticas
Pesquisas eleitorais e de opinião pública
Institutos de pesquisa usam intervalos de confiança para estimar a intenção de voto. Se um candidato tem 40% das intenções, com um intervalo de 38% a 42% e 95% de confiança, isso significa que, em 95% das amostras, o verdadeiro apoio ao candidato estará dentro dessa faixa.
Pesquisas de opinião seguem a mesma lógica. Uma empresa pode medir a satisfação de clientes e encontrar um índice de 85% de aprovação, com intervalo entre 83% e 87%, ajudando a entender a percepção do público com um grau de certeza definido.
Estudos científicos e testes de hipóteses
Pesquisas científicas utilizam intervalos de confiança para validar hipóteses. Em um teste clínico, um novo medicamento pode reduzir a pressão arterial em 10 mmHg, com um intervalo de 8 a 12 mmHg. Se o intervalo não incluir zero, há evidências de que o tratamento tem efeito significativo.
Essa abordagem evita conclusões precipitadas e reforça a confiabilidade dos resultados.
2. Uso em controle de qualidade e indústria
Controle estatístico de processos
Na indústria, intervalos de confiança monitoram a qualidade da produção. Se uma fábrica de parafusos deseja garantir que o comprimento médio seja 5 cm, ela coleta amostras e encontra um intervalo de 4,98 cm a 5,02 cm. Se esse intervalo estiver dentro dos limites aceitáveis, o processo está sob controle.
Caso o intervalo seja muito amplo, indicando variação excessiva, ajustes no maquinário podem ser necessários para evitar produtos fora do padrão.
Garantia de conformidade com padrões
Normas como a ISO 9001 exigem controle de variações. Em uma indústria de alimentos, se o teor de sódio de um produto precisa ser 500 mg por porção, mas a análise indica um intervalo de 480 mg a 520 mg, a empresa deve avaliar se isso atende às exigências regulatórias.
Se o intervalo ultrapassa os limites permitidos, ajustes na formulação ou no controle de processos podem ser necessários.
3. Intervalo de confiança em finanças e negócios
Projeções de risco e retorno
Investidores utilizam intervalos de confiança para estimar retornos financeiros. Se um fundo de investimentos prevê um retorno anual de 8%, com um intervalo entre 6% e 10%, isso indica um nível de incerteza sobre a rentabilidade real.
Intervalos menores sugerem maior previsibilidade, enquanto intervalos amplos indicam maior volatilidade e risco.
Análise de mercado e estudos de viabilidade
Empresas utilizam intervalos de confiança para projetar demanda de produtos. Se uma pesquisa estima que um novo lançamento terá 10 mil unidades vendidas no primeiro mês, com um intervalo entre 9 mil e 11 mil, isso ajuda no planejamento de estoque e produção.
Um intervalo muito amplo pode indicar que o mercado é imprevisível, demandando mais estudos antes de uma decisão estratégica.
Leia mais:





