O que é o Teorema de Bayes?
Em nosso Black Belt, um dos temas que trazemos à tona é probabilidade. E, ao falar em probabilidade, precisamos falar de Bayes. O inglês Thomas Bayes foi um pastor protestante, provavelmente nascido em 1701. Sabe-se pouco a respeito de sua vida, apesar de ele dar nome a todo um campo da estatística e talvez seu mais famoso teorema.
Sua obra mais famosa foi Essay toward Solving a Problem in the Doctrine of Chances (Tentativa de elucidar um problema na doutrina do acaso), publicada somente depois de sua morte. Seu tema tratava de como formular convicções probabilísticas a respeito do mundo quando diante de novos dados.
Na introdução sobre obra, seu amigo Richard Price, toma como exemplo o caso de uma pessoa que surge no mundo (talvez Adão, talvez alguém saído da caverna de Platão) e vê o nascer do sol pela primeira vez. A princípio, ele não sabe se é um fenômeno típico ou algum episódio insólito. Porém, a cada dia que sobrevive e vê o nascer do sol, aumenta sua confiança de que se trata de uma característica permanente da natureza. Aos poucos, por meio dessa forma de dedução apenas estatística, a probabilidade que ele aplica à previsão de que o sol irá nascer no dia seguinte se aproxima de 100%, embora nunca chegue a esse ponto.
O argumento desenvolvido por Bayes não afirma que o mundo é, de forma intrínseca, probabilístico ou incerto. Bayes acreditava na perfeição divina e defendia a obra de Isaac Newton, que parecia sugerir que a natureza segue leis regulares e previsíveis. O que Bayes faz é uma afirmação matemático filosófica sobre como aprendemos a respeito do universo: por meio de estimativas, aproximando-nos cada vez mais e mais da verdade à medida que reunimos mais indícios.
O ponto de vista bayesiano considera a racionalidade uma questão probabilística. “Não culpe a natureza por você ser tolo demais para compreendê-la: se sair de sua concha de ceticismo e fizer algumas previsões sobre o comportamento dela, talvez chegue um pouco mais perto da verdade”.
Mas de onde veio o teorema de Bayes?
O teorema de Bayes foi desenvolvido por um homem brilhante, o matemático e astrônomo francês Pierre-Simon Laplace. Ele, argumentava ser possível prever o universo de forma perfeita, mas para isto deveríamos saber a posição de cada partícula em seu interior e teríamos de ser rápidos o bastante para calcular seus movimentos. Por que, então, Laplace envolveu-se com uma teoria que é conhecida como a base do “probabilismo”?
Na época, Laplace estava frustrado com suas observações astronômicas que pareciam mostrar anomalias nas órbitas de Jupiter e Saturno, pois previam que Júpiter iria colidir com o Sol, enquanto Saturno ficaria à deriva no espaço. Claro que tais previsões estavam erradas, mas Laplace então dedicou-se a melhorar suas previsões, principalmente no que tocavam suas deduções a partir de probabilidades, ao invés de trabalhar com medidas mais precisas. Para ele, estava claro que entender melhor as questões acerca da probabilidade eram fundamentais para o progresso científico.
A matemática por trás do teorema de Bayes
Em sua forma mais básica, trata-se apenas de uma expressão algébrica com quatro variáveis – três conhecidas e uma desconhecida. Porém, apesar de sua simplicidade, ela pode nos conduzir a vastas percepções no âmbito das previsões. O foco do teorema é a probabilidade condicionada. Ou seja, fala da probabilidade de uma teoria ou hipótese ser verdadeira se tiver havido determinado acontecimento.
Imagine que você seja um rapaz que mora com sua namorada. Voltando de uma viagem de negócios, você tem uma surpresa. Encontra uma cueca desconhecida na gaveta do armário. Automaticamente, seu cérebro irá se perguntar: qual é a probabilidade de eu ter sido traído? A condição encontrada é a roupa íntima encontrada; a hipótese que você deseja considerar é uma traição. O teorema de Bayes, acredite ou não, é a melhora forma de você abordar este constrangedor questionamento, mas para isto, você terá que saber algumas coisas:
- Qual a probabilidade da aparição de uma roupa íntima numa condição em que a hipótese seja verdadeira – ou seja, em que houve mesma a traição? Se ela está traindo você, não seria difícil imaginar como a cueca foi parar na gaveta. Então, mesmo que ela esteja te traindo, você imagina que fosse mais cuidadosa. Digamos que a probabilidade de a cueca aparecer, como condição para ela estar enganando, é de 50%.
- Qual a probabilidade de surgimento da cueca numa condição em que a hipótese seja falsa? Se ela não está te traindo, existe alguma explicação inocente para justificar a cuecona ali? É claro que as hipóteses são mais complicadas, como sua mulher decidiu agora usar cuecas, ou um amigo dela, gente boa, foi passar a noite com ela. Poderia ser um presente, do dia dos namorados, para você que ela esqueceu de embrulhar. Nenhuma destas teorias são insustentáveis, mas parecem um pouco as explicações sobre a Lava Jato, então, você calcula uns 5%.
- O último e mais importante, é a probabilidade prévia. Em quanto você estimaria a probabilidade de uma traição antes de encontrar a cueca? Temos que ser objetivos sobre esta probabilidade e esquecer a raiva momentânea. Se conseguirmos acessar os dados disponíveis, veremos que cerca de 14,7% segundo um estudo do General Social Survey das mulheres americanas traem. Mas como somos brasileiros, corre uma pesquisa de que o percentual era de 56,4%. Fico um pouco preocupado com este estudo e vou estimar um meio a meio. Que tal considerar que 30% das mulheres traem?
Uma vez estimados esses números, o teorema de Bayes pode ser aplicado para estabelecermos uma probabilidade posterior. Esse é o número que em estamos interessados: qual a probabilidade de uma traição, levando em conta que encontramos uma cueca no armário de casa?
- Estimativa inicial das chances de traição: x = 30%
- Fato novo: cueca encontrada
- Probabilidade de surgimento da cueca como condição para traição: y = 50%
- Probabilidade do surgimento da cueca se não houver traição: z = 5%
- Probabilidade Posterior
- Estimativa revisada da probabilidade de traição, considerando que você achou a cueca
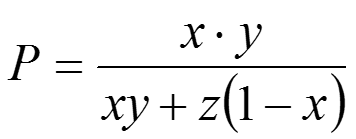
- P = 81%
Pelo teorema de Bayes, a probabilidade de você estar sendo traído é de 81%, o que é na minha opinião é bastante alta. Neste caso, quem manda na equação é probabilidade inicial de estar ocorrendo a traição. Se, por ventura, você encontrasse um estudo que estimasse a probabilidade de uma mulher trair em 4%, a probabilidade de você estar sendo traído iria cair para 29%, o que é muito mais confortável, se você for o homem. Porém, se adotássemos os 56,4% do estudo que encontramos sobre as mulheres brasileiras, o número subiria para 83%, o que não parece um aumento crucial para sua tomada de decisão. Neste mesmo estudo, falava-se que 70% dos homens traiam. Neste caso, ao encontrar uma calcinha na sua casa, cara leitora, se aplicar o teorema, seu marido ficará em maus lençóis.
Hoje, poderíamos aumentar a precisão de sua estimativa se fossemos analisando mais a fundo as características da sua mulher. Quanto mais apurada for a probabilidade prévia, melhor será a sua assertividade na probabilidade posterior. Porém, não quero sugerir que nossas probabilidades prévias sempre prevaleçam sobre indícios novos ou que o teorema de Bayes produz, por si só, resultados que podem ser contrários aos nossos instintos. Às vezes, as novas evidências são tão fortes que ofuscam todo o resto, fazendo com que possamos passar, de forma praticamente instantânea, de uma probabilidade próxima de zero a uma quase certeza.
O teorema de Bayes não é uma formula mágica – em sua forma simples empregada aqui, é álgebra básica. Precisamos, no entanto, abastecê-lo com informações de qualidade, em particular, nossas estimativas sobre probabilidades prévias, para que ele nos entregue resultados úteis.
A maior lição do teorema de Bayes é que ele nos exige que pensemos de forma probabilística a respeito do mundo, mesmo ao lidarmos com temas que não gostamos de considerar como determinados pelo acaso. Isso não significa que tenhamos de encarar o mundo como algo incerto de forma intrínseca ou metafisica (a lá Montanha Mágica). Laplace, que acreditava que tudo, das órbitas dos planetas ao comportamento das partículas, era governado por metódicas regras newtonianas, mudou seu entendimento e teve um papel fundamental no desenvolvimento do Teorema de Bayes. Esta é a melhor forma de lidarmos com a incerteza epistemológica, com os limites de nosso conhecimento.





